Το θέμα του σημερινού μας άρθρου θα είναι η κινηματική ενός υλικού σημείου. Τι είναι αυτό; Ποιες έννοιες εμφανίζονται σε αυτό και ποιος ορισμός πρέπει να δοθεί σε αυτόν τον όρο; Θα προσπαθήσουμε να απαντήσουμε σε αυτές και σε πολλές άλλες ερωτήσεις σήμερα.
Ορισμός και έννοια
Η κινηματική ενός υλικού σημείου δεν είναι τίποτα άλλο από μια υποενότητα της φυσικής που ονομάζεται «μηχανική». Αυτή, με τη σειρά της, μελετά τα μοτίβα κίνησης ορισμένων σωμάτων. Η κινηματική ενός υλικού σημείου ασχολείται επίσης με αυτό το πρόβλημα, αλλά δεν το κάνει με γενικό τρόπο. Στην πραγματικότητα, αυτή η υποενότητα μελετά μεθόδους που σας επιτρέπουν να περιγράψετε την κίνηση των σωμάτων. Σε αυτή την περίπτωση, μόνο τα λεγόμενα εξιδανικευμένα σώματα είναι κατάλληλα για έρευνα. Αυτά περιλαμβάνουν: ένα υλικό σημείο, ένα απολύτως άκαμπτο σώμα και ένα ιδανικό αέριο. Ας εξετάσουμε τις έννοιες με περισσότερες λεπτομέρειες. Όλοι γνωρίζουμε από το σχολικό παγκάκι ότι συνηθίζεται να ονομάζουμε ένα υλικό σημείο σώμα, οι διαστάσεις του οποίου σε μια δεδομένη κατάσταση μπορούν να παραμεληθούν. Παρεμπιπτόντως, ξεκινά η κινηματική της μεταφορικής κίνησης ενός υλικού σημείου για πρώτη φοράεμφανίζονται στα εγχειρίδια φυσικής της έβδομης δημοτικού. Αυτός είναι ο απλούστερος κλάδος, επομένως είναι πιο βολικό να ξεκινήσετε τη γνωριμία με την επιστήμη με τη βοήθειά του. Ένα ξεχωριστό ερώτημα είναι ποια είναι τα στοιχεία της κινηματικής ενός υλικού σημείου. Υπάρχουν πολλά από αυτά και υπό όρους μπορούν να χωριστούν σε πολλά επίπεδα με διαφορετική πολυπλοκότητα για κατανόηση. Αν μιλάμε, για παράδειγμα, για το διάνυσμα ακτίνας, τότε, καταρχήν, δεν υπάρχει τίποτα απαγορευτικά περίπλοκο στον ορισμό του. Ωστόσο, θα συμφωνήσετε ότι θα είναι πολύ πιο εύκολο για έναν μαθητή να το καταλάβει παρά για έναν μαθητή Γυμνασίου ή Λυκείου. Και για να είμαι ειλικρινής, δεν χρειάζεται να εξηγήσουμε τα χαρακτηριστικά αυτού του όρου σε μαθητές γυμνασίου.
Μια σύντομη ιστορία της δημιουργίας της κινηματικής
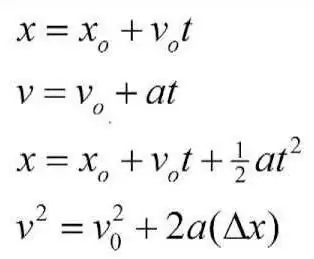
Πριν από πολλά, πολλά χρόνια, ο μεγάλος επιστήμονας Αριστοτέλης αφιέρωσε τη μερίδα του λέοντος από τον ελεύθερο χρόνο του στη μελέτη και την περιγραφή της φυσικής ως ξεχωριστής επιστήμης. Εργάστηκε επίσης στην κινηματική, προσπαθώντας να παρουσιάσει τις κύριες θέσεις και έννοιές της, με τον ένα ή τον άλλο τρόπο που χρησιμοποιούνται σε προσπάθειες επίλυσης πρακτικών, ακόμη και καθημερινών προβλημάτων. Ο Αριστοτέλης έδωσε τις αρχικές ιδέες για το ποια είναι τα στοιχεία της κινηματικής ενός υλικού σημείου. Τα έργα και τα έργα του είναι πολύτιμα για όλη την ανθρωπότητα. Ωστόσο, στα συμπεράσματά του έκανε έναν σημαντικό αριθμό λαθών και ο λόγος για αυτό ήταν ορισμένες παρανοήσεις και λάθος υπολογισμοί. Κάποια στιγμή, ένας άλλος επιστήμονας, ο Galileo Galilei, ενδιαφέρθηκε για τα έργα του Αριστοτέλη. Μία από τις θεμελιώδεις θέσεις που διατύπωσε ο Αριστοτέλης ήταν ότι η κίνηση ενός σώματοςεμφανίζεται μόνο εάν ασκείται από κάποια δύναμη, που καθορίζεται από την ένταση και την κατεύθυνση. Ο Γαλιλαίος απέδειξε ότι αυτό ήταν λάθος. Η δύναμη θα επηρεάσει την παράμετρο ταχύτητας κίνησης, αλλά όχι περισσότερο. Ο Ιταλός έδειξε ότι η δύναμη είναι η αιτία της επιτάχυνσης και μπορεί να προκύψει μόνο αμοιβαία με αυτήν. Επίσης, ο Galileo Galilei έδωσε μεγάλη προσοχή στη μελέτη της διαδικασίας της ελεύθερης πτώσης, αντλώντας τα κατάλληλα μοτίβα. Μάλλον όλοι θυμούνται τα περίφημα πειράματά του, τα οποία έκανε στον Πύργο της Πίζας. Ο φυσικός Ampère χρησιμοποίησε επίσης τα βασικά των κινηματικών λύσεων στα έργα του.
Αρχικές έννοιες
Όπως αναφέρθηκε προηγουμένως, η κινηματική είναι η μελέτη τρόπων περιγραφής της κίνησης εξιδανικευμένων αντικειμένων. Σε αυτή την περίπτωση, τα βασικά στοιχεία της μαθηματικής ανάλυσης, της συνηθισμένης άλγεβρας και της γεωμετρίας μπορούν να εφαρμοστούν στην πράξη. Ποιες όμως έννοιες (ακριβώς έννοιες και όχι ορισμοί για παραμετρικά μεγέθη) αποτελούν τη βάση αυτής της υποενότητας της φυσικής; Πρώτον, όλοι πρέπει να κατανοήσουν ξεκάθαρα ότι η κινηματική της μεταφορικής κίνησης ενός υλικού σημείου εξετάζει την κίνηση χωρίς να λαμβάνει υπόψη τους δείκτες δύναμης. Δηλαδή, για να λύσουμε τα αντίστοιχα προβλήματα, δεν χρειαζόμαστε τύπους που σχετίζονται με τη δύναμη. Δεν λαμβάνεται υπόψη από την κινηματική, ανεξάρτητα από το πόσα από αυτά υπάρχουν - ένα, δύο, τρία, τουλάχιστον αρκετές εκατοντάδες χιλιάδες. Παρόλα αυτά η ύπαρξη επιτάχυνσης εξακολουθεί να παρέχεται. Σε μια σειρά προβλημάτων, η κινηματική της κίνησης ενός υλικού σημείου προβλέπει τον προσδιορισμό του μεγέθους της επιτάχυνσης. Ωστόσο, οι αιτίες αυτού του φαινομένου (δηλαδή οι δυνάμεις καιη φύση τους) δεν λαμβάνονται υπόψη αλλά παραλείπονται.
Ταξινόμηση
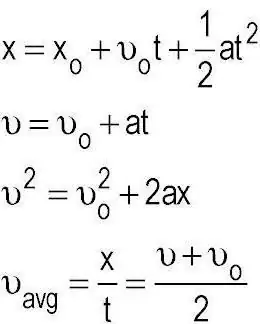
Διαπιστώσαμε ότι η κινηματική εξερευνά και εφαρμόζει μεθόδους για να περιγράψει την κίνηση των σωμάτων χωρίς να λαμβάνει υπόψη τις δυνάμεις που ασκούν πάνω τους. Παρεμπιπτόντως, μια άλλη υποενότητα της μηχανικής, η οποία ονομάζεται δυναμική, ασχολείται με μια τέτοια εργασία. Ήδη εκεί εφαρμόζονται οι νόμοι του Νεύτωνα, οι οποίοι επιτρέπουν στην πράξη τον προσδιορισμό πολλών παραμέτρων με μια μικρή ποσότητα γνωστών αρχικών δεδομένων. Οι βασικές έννοιες της κινηματικής ενός υλικού σημείου είναι ο χώρος και ο χρόνος. Και σε σχέση με την ανάπτυξη της επιστήμης τόσο γενικά όσο και σε αυτόν τον τομέα, προέκυψε το ερώτημα σχετικά με την καταλληλότητα χρήσης ενός τέτοιου συνδυασμού.
Από την αρχή υπήρχε η κλασική κινηματική. Μπορούμε να πούμε ότι χαρακτηρίζεται όχι μόνο από την παρουσία τόσο χρονικών όσο και χωρικών κενών, αλλά και από την ανεξαρτησία τους από την επιλογή του ενός ή του άλλου πλαισίου αναφοράς. Παρεμπιπτόντως, θα μιλήσουμε για αυτό λίγο αργότερα. Τώρα ας εξηγήσουμε για τι πράγμα μιλάμε. Σε αυτήν την περίπτωση, ένα τμήμα θα θεωρείται ως χωρικό διάστημα και ένα χρονικό διάστημα θα θεωρείται ως χρονικό διάστημα. Όλα δείχνουν να είναι ξεκάθαρα. Έτσι, αυτά τα κενά θα θεωρηθούν στην κλασική κινηματική ως απόλυτα, αμετάβλητα, με άλλα λόγια, ανεξάρτητα από τη μετάβαση από το ένα πλαίσιο αναφοράς στο άλλο. Είτε επιχειρηματική σχετικιστική κινηματική. Σε αυτό, τα κενά κατά τη μετάβαση μεταξύ συστημάτων αναφοράς μπορούν να αλλάξουν. Θα ήταν ακόμη πιο σωστό να πούμε ότι δεν μπορούν, αλλά μάλλον πρέπει. Εξαιτίας αυτού, ο ταυτόχρονος των δύοΤα τυχαία συμβάντα γίνονται επίσης σχετικά και υπόκεινται σε ειδική εξέταση. Γι' αυτό στη σχετικιστική κινηματική δύο έννοιες - χώρος και χρόνος - συνδυάζονται σε μία.
Κινηματική ενός υλικού σημείου: ταχύτητα, επιτάχυνση και άλλες ποσότητες
Για να κατανοήσετε τουλάχιστον λίγο αυτήν την υποενότητα της φυσικής, πρέπει να περιηγηθείτε στις πιο σημαντικές έννοιες, να γνωρίζετε τους ορισμούς και να φανταστείτε ποια είναι αυτή ή η ποσότητα σε γενικές γραμμές. Δεν υπάρχει τίποτα δύσκολο σε αυτό, στην πραγματικότητα, όλα είναι πολύ εύκολα και απλά. Σκεφτείτε, ίσως, αρχικά, τις βασικές έννοιες που χρησιμοποιούνται στα κινηματικά προβλήματα.
Movement
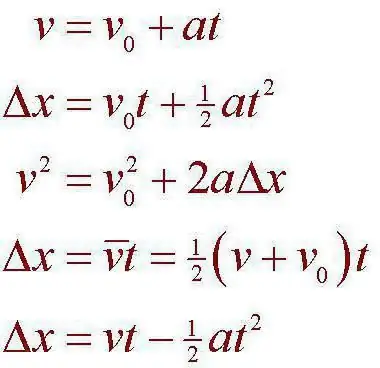
Μηχανική κίνηση θα εξετάσουμε τη διαδικασία κατά την οποία ένα ή άλλο εξιδανικευμένο αντικείμενο αλλάζει τη θέση του στο χώρο. Σε αυτή την περίπτωση, μπορούμε να πούμε ότι η αλλαγή συμβαίνει σε σχέση με άλλα σώματα. Είναι επίσης απαραίτητο να ληφθεί υπόψη το γεγονός ότι ο καθορισμός ενός συγκεκριμένου χρονικού διαστήματος μεταξύ δύο γεγονότων συμβαίνει ταυτόχρονα. Για παράδειγμα, θα είναι δυνατό να απομονωθεί ένα ορισμένο διάστημα που σχηματίστηκε κατά τη διάρκεια του χρόνου που μεσολάβησε μεταξύ της άφιξης του σώματος από τη μια θέση στην άλλη. Σημειώνουμε επίσης ότι τα σώματα σε αυτή την περίπτωση μπορούν και θα αλληλεπιδράσουν μεταξύ τους, σύμφωνα με τους γενικούς νόμους της μηχανικής. Με αυτό ακριβώς λειτουργεί συχνότερα η κινηματική ενός υλικού σημείου. Το σύστημα αναφοράς είναι η επόμενη έννοια που είναι άρρηκτα συνδεδεμένη με αυτό.
Συντεταγμένες
Μπορούν να ονομαστούν συνηθισμένα δεδομένα που σας επιτρέπουν να προσδιορίσετε τη θέση του σώματος τη μία ή την άλλη στιγμή. Οι συντεταγμένες είναι άρρηκτα συνδεδεμένες με την έννοια του συστήματος αναφοράς, καθώς και με το πλέγμα συντεταγμένων. Τις περισσότερες φορές είναι ένας συνδυασμός γραμμάτων και αριθμών.
Διάνυσμα ακτίνας
Από το όνομα θα πρέπει ήδη να είναι ξεκάθαρο τι είναι. Ωστόσο, ας μιλήσουμε για αυτό με περισσότερες λεπτομέρειες. Εάν ένα σημείο κινείται κατά μήκος μιας συγκεκριμένης τροχιάς και γνωρίζουμε ακριβώς την αρχή ενός συγκεκριμένου συστήματος αναφοράς, τότε μπορούμε να σχεδιάσουμε ένα διάνυσμα ακτίνας ανά πάσα στιγμή. Θα συνδέσει την αρχική θέση του σημείου με τη στιγμιαία ή την τελική θέση.
Trajectory
Θα ονομάζεται συνεχής γραμμή, η οποία τοποθετείται ως αποτέλεσμα της κίνησης ενός υλικού σημείου σε ένα συγκεκριμένο σύστημα αναφοράς.
Ταχύτητα (τόσο γραμμική όσο και γωνιακή)
Αυτή είναι μια τιμή που μπορεί να πει πόσο γρήγορα διανύει το σώμα ένα συγκεκριμένο διάστημα απόστασης.
Επιτάχυνση (τόσο γωνιακή όσο και γραμμική)
Δείχνει με ποιο νόμο και πόσο έντονα αλλάζει η παράμετρος ταχύτητας του σώματος.
Ίσως, εδώ είναι - τα κύρια στοιχεία της κινηματικής ενός υλικού σημείου. Πρέπει να σημειωθεί ότι τόσο η ταχύτητα όσο και η επιτάχυνση είναι διανυσματικά μεγέθη. Και αυτό σημαίνει ότι δεν έχουν μόνο κάποια ενδεικτική αξία, αλλά και μια συγκεκριμένη κατεύθυνση. Παρεμπιπτόντως, μπορούν να κατευθυνθούν τόσο προς μία κατεύθυνση όσο και προς αντίθετες κατευθύνσεις. Στην πρώτη περίπτωση, το σώμα θα επιταχύνει, στη δεύτερη θα επιβραδύνει.
Απλές εργασίες
Η κινηματική ενός υλικού σημείου (ταχύτητα, επιτάχυνση και απόσταση που είναι πρακτικά θεμελιώδεις έννοιες) περιλαμβάνει όχι μόνο έναν τεράστιο αριθμό εργασιών, αλλά πολλές από τις διαφορετικές κατηγορίες τους. Ας προσπαθήσουμε να λύσουμε ένα αρκετά απλό πρόβλημα προσδιορίζοντας την απόσταση που διανύει το σώμα.
Ας υποθέσουμε ότι οι συνθήκες που έχουμε στη διάθεσή μας είναι οι εξής. Το αυτοκίνητο του οδηγού βρίσκεται στη γραμμή εκκίνησης. Ο χειριστής δίνει το πράσινο φως με τη σημαία και το αυτοκίνητο απογειώνεται απότομα. Προσδιορίστε εάν μπορεί να σημειώσει νέο ρεκόρ στον αγώνα των δρομέων, εάν ο επόμενος αρχηγός κάλυψε μια απόσταση εκατό μέτρων σε 7,8 δευτερόλεπτα. Πάρτε την επιτάχυνση του αυτοκινήτου ίση με 3 μέτρα διαιρούμενο με το τετράγωνο του δευτερολέπτου.
Λοιπόν, πώς να λύσετε αυτό το πρόβλημα; Είναι αρκετά ενδιαφέρον, αφού απαιτείται να μην «στεγνώσουμε» ορισμένες παραμέτρους. Φωτίζεται με τζίρους και μια συγκεκριμένη κατάσταση, η οποία διαφοροποιεί τη διαδικασία επίλυσης και αναζήτησης δεικτών. Αλλά από τι πρέπει να καθοδηγούμαστε πριν προσεγγίσουμε την εργασία;
1. Η κινηματική ενός υλικού σημείου προβλέπει τη χρήση της επιτάχυνσης σε αυτή την περίπτωση.
2. Η λύση θεωρείται ότι χρησιμοποιεί τον τύπο της απόστασης, καθώς η αριθμητική της τιμή εμφανίζεται στις συνθήκες.
Το πρόβλημα στην πραγματικότητα λύνεται πολύ απλά. Για να γίνει αυτό, παίρνουμε τον τύπο απόστασης: S=VoT + (-) AT ^ 2/2. Ποιο είναι το νόημα? Πρέπει να μάθουμε πόσο καιρό θα διανύσει ο αναβάτης την καθορισμένη απόσταση και, στη συνέχεια, να συγκρίνουμε τη φιγούρα με το ρεκόρ για να μάθουμε αν το κερδίζει ή όχι. Για να το κάνετε αυτό, διαθέστε χρόνο, λαμβάνουμε τον τύπογια αυτόν: AT^2 + 2VoT - 2S. Αυτό δεν είναι τίποτα άλλο από μια τετραγωνική εξίσωση. Αλλά το αυτοκίνητο απογειώνεται, πράγμα που σημαίνει ότι η αρχική ταχύτητα θα είναι 0. Κατά την επίλυση της εξίσωσης, η διάκριση θα είναι ίση με 2400. Για να βρείτε το χρόνο, πρέπει να πάρετε τη ρίζα. Ας το κάνουμε με το δεύτερο δεκαδικό ψηφίο: 48,98 Βρείτε τη ρίζα της εξίσωσης: 48,98/6=8,16 δευτερόλεπτα. Αποδεικνύεται ότι ο οδηγός δεν θα μπορέσει να κερδίσει το υπάρχον ρεκόρ.






