Για να μπορέσουν να απεικονίσουν σε χαρτί αντικείμενα που στην πραγματικότητα δεν έχουν πολύ «βολικά» μεγέθη, οι άνθρωποι βρήκαν μια κλίμακα. Στην πραγματικότητα, αυτό εξηγεί σε τι χρησιμεύει η ζυγαριά.
Όταν το σχολικό πρόγραμμα αρχίζει να αποκαλύπτει την έννοια της κλίμακας
Για πρώτη φορά, τα παιδιά συναντούν αυτή τη λέξη ενώ μελετούν χάρτες και σχέδια της περιοχής. Ο δάσκαλος εξηγεί γιατί χρειάζεται η κλίμακα, τι δείχνει, χρησιμοποιώντας άτλαντες ως παράδειγμα. Εξηγείται ότι οποιοδήποτε γεωγραφικό χαρακτηριστικό είναι τόσο μεγάλο που θα ήταν δύσκολο και άβολο να το απεικονίσεις σε πλήρες μέγεθος.
Οι άνθρωποι σχεδίασαν το έδαφος σε μειωμένη μορφή, αλλά για αυτό δεν χρησιμοποίησαν ακριβείς αναλογίες. Τώρα γίνεται πιο έξυπνα - κάθε παύλα και γραμμή που απεικονίζονται στον χάρτη έχουν ένα μέγεθος που μπορεί να πολλαπλασιαστεί με έναν ορισμένο αριθμό και να ανακαλύψει το πραγματικό μήκος και πλάτος.
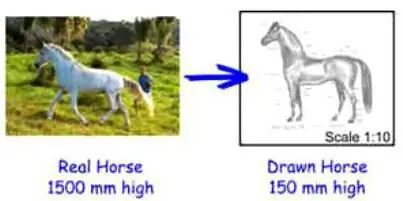
Κλίμακα εγγραφής: ο πρώτος τρόπος ανάγνωσης
Η κλίμακα υποδεικνύεται με δύο αριθμούς που χωρίζονται με άνω και κάτω τελεία. Το πρώτο ψηφίο δείχνει τις μονάδες διάστασης στο σχήμα, το δεύτεροδείχνει πόσες πραγματικές μονάδες στο σχήμα αντιστοιχεί στον πρώτο αριθμό. Για παράδειγμα, εάν σε κάποιο σχέδιο υποδεικνύεται μια κλίμακα 1:1000 και οι μονάδες διαστάσεων υποδεικνύονται σε εκατοστά, τότε ένα εκατοστό στο σχήμα αντιστοιχεί σε 1000 cm στην πραγματικότητα. Προς τι λοιπόν η ζυγαριά; Με τη βοήθειά του, μπορείτε όχι μόνο να μειώσετε ορισμένα αντικείμενα στο γραφικό σχέδιο, αλλά και να υπολογίσετε με ακρίβεια το πραγματικό τους μέγεθος.
Ο δεύτερος τρόπος καταγραφής της κλίμακας: τι είναι βολικό;
Η προηγούμενη μέθοδος εγγραφής της κλίμακας μέσω άνω και κάτω τελείας ονομάζεται αριθμητική. Υπάρχει όμως και μια ονομαστική κλίμακα. Το ρεκόρ του έχει ως εξής: 1 cm - 20 km. Αποδεικνύεται ότι με αυτόν τον τρόπο είναι δυνατό να γράψετε συμπαγή τεράστιες κλίμακες που δεν θα εκφραστούν με αριθμούς με πολλά μηδενικά, εάν έχει συμβεί μια κατάσταση όταν είναι απαραίτητο να υποδειχθούν αρκετές εκατοντάδες χιλιόμετρα σε ένα εκατοστό. Ταυτόχρονα, γίνεται αμέσως σαφές πόσο, τι και σε τι. Αυτό το αρχείο είναι πιο διαισθητικό και σαφές.
Κλιμάκωση στο σχέδιο: τι συμπληρώνει την έννοια που μελετήθηκε προηγουμένως
Η έννοια της κλίμακας συναντάται όχι μόνο στη γεωγραφία, αλλά και στη μελέτη ενός θέματος όπως το σχέδιο. Οι ίδιες αρχές χρησιμοποιούνται για την απεικόνιση διαφόρων αντικειμένων. Αλλά υπάρχει μια σημαντική διαφορά: εδώ η έννοια του τι είναι η κλίμακα διευρύνεται επίσης από το γεγονός ότι μπορεί να χρησιμοποιηθεί για την απεικόνιση μικρών λεπτομερειών σε μεγαλύτερη κλίμακα. Στη γεωγραφία, δεν μιλάμε για αυτό, γιατί δεν υπάρχουν τόσο μικρά αντικείμενα στη γεωγραφία που να χρειάζεται να τα μεγεθύνουμε. Οι ήπειροι και τα βουνά, τα ποτάμια και οι λίμνες είναι σε κάθε περίπτωση μεγαλύτερα από φύλλα χαρτιού Α4 ή ακόμα καιA1.
Μελετώντας το σχέδιο, μπορείτε να χρησιμοποιήσετε την κλίμακα για να απεικονίσετε σε μεγαλύτερη μορφή τις μικρότερες λεπτομέρειες, όπως ένα μπουλόνι ή ένα γρανάζι.
Λοιπόν, γιατί χρειαζόμαστε μια ζυγαριά σε αυτήν την περίπτωση; Με τη βοήθειά του, μπορείτε να απεικονίσετε πιο άνετα, καθαρά και λεπτομερώς ένα μικρό στοιχείο. Σε αυτήν την περίπτωση, συμβαίνει το αντίστροφο στον συμβολισμό: ο πρώτος αριθμός θα είναι μεγαλύτερος από τον δεύτερο και ο συμβολισμός 100:1 θα ακούγεται κάπως έτσι: 100 μετρικές μονάδες της εικόνας αντιστοιχούν σε μία μονάδα του πραγματικού μεγέθους.
Μερικά διευκρινιστικά παραδείγματα
Τι είναι η κλίμακα, τι δείχνει στην περίπτωση μιας εικόνας ενός μικρότερου αντικειμένου, ποιο είναι το αποτέλεσμα σε χαρτί; Και πάλι, έχουμε την ακριβή αναλογία των διαστάσεων της εικόνας του εξαρτήματος και του πραγματικού αντικειμένου. Θυμηθείτε την ίδια κλίμακα 100:1. Αποδεικνύεται ότι σε εκατό χιλιοστά στο σχήμα υπάρχει μόνο ένα χιλιοστό πραγματικού μεγέθους. Εάν ένα εξάρτημα έχει πλάτος 500 χιλιοστά στην εικόνα, το πραγματικό του πλάτος είναι μόνο 5 χιλιοστά.
Αν θυμηθούμε την πρώτη περίπτωση, την εικόνα σε ένα φύλλο ενός μικρότερου αντιγράφου ενός μεγάλου αντικειμένου, η κλίμακα 1:100 θα σημαίνει ότι ένα χιλιοστό στην εικόνα περιέχει 100 χιλιοστά του πραγματικού μεγέθους. Έτσι, εάν ένα αντικείμενο έχει μήκος 80 χιλιοστά σε ένα σχέδιο ή χάρτη, το πραγματικό μήκος του αντικειμένου θα είναι 8000 χιλιοστά. Ένα ξεκάθαρο παράδειγμα του τι χρησιμεύει η ζυγαριά και τι βολική εφεύρεση της ανθρωπότητας.
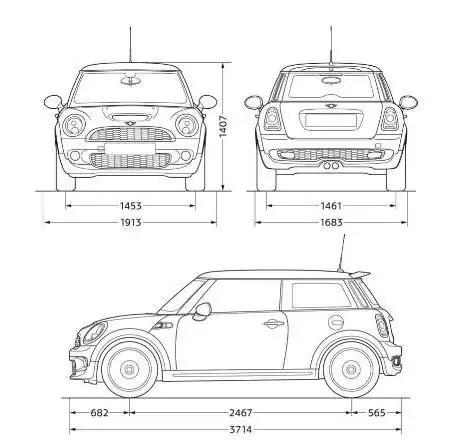
Το κύριο πράγμα στη χρήση της ζυγαριάς είναι αμέσωςνα θυμάστε ότι ο πρώτος αριθμός αναφέρεται στην εικόνα και ο δεύτερος στο πραγματικό μέγεθος των αντικειμένων. Για να μην μπερδευτούμε στο μέλλον, για να εδραιωθούν αυτά τα θεμέλια, γίνονται πρακτικά μαθήματα γεωγραφίας στα σχολεία, ώστε τα παιδιά να εξηγούν και να υπολογίζουν τα μεγέθη των πραγματικών αντικειμένων πολλές φορές χρησιμοποιώντας τον άτλαντα. Το ίδιο συμβαίνει και στα μαθήματα ζωγραφικής.
Σύνοψη
Που είναι η ζυγαριά; Η απάντηση σε αυτήν την ερώτηση αποτελείται από τρία σημεία που πρέπει απλώς να θυμάστε:
- Πρώτα - η κλίμακα είναι απαραίτητη για την εμφάνιση μεγάλων αντικειμένων σε μια επιφάνεια που είναι βολική για προβολή.
- Δεύτερο - η κλίμακα είναι απαραίτητη για να απεικονίζονται μικρά αντικείμενα σε μεγαλύτερο μέγεθος.
- Τρίτο - η κλίμακα είναι απαραίτητη για να μπορούμε να προσδιορίσουμε με ακρίβεια το μέγεθος ενός πραγματικού αντικειμένου, ανεξάρτητα από το αρχικό του μέγεθος, μικρό ή μεγάλο.






