Η θερμοχωρητικότητα ενός αερίου είναι η ποσότητα ενέργειας που απορροφά ένα σώμα όταν θερμαίνεται κατά ένα βαθμό. Ας αναλύσουμε τα κύρια χαρακτηριστικά αυτής της φυσικής ποσότητας.

Ορισμοί
Η ειδική θερμότητα ενός αερίου είναι η μονάδα μάζας μιας συγκεκριμένης ουσίας. Οι μονάδες μέτρησής του είναι J/(kg·K). Η ποσότητα θερμότητας που απορροφάται από το σώμα κατά τη διαδικασία αλλαγής της κατάστασης συσσώρευσής του σχετίζεται όχι μόνο με την αρχική και τελική κατάσταση, αλλά και με τη μέθοδο μετάβασης.

Τμήμα
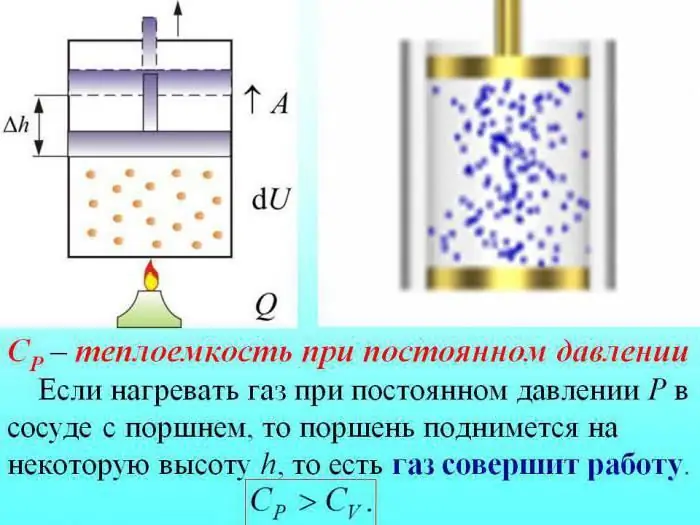
Η θερμοχωρητικότητα των αερίων διαιρείται με την τιμή που προσδιορίζεται σε σταθερό όγκο (Cv), σταθερή πίεση (Cр).
Σε περίπτωση θέρμανσης χωρίς αλλαγή της πίεσης, λίγη θερμότητα δαπανάται για να παραχθεί το έργο της διαστολής του αερίου και μέρος της ενέργειας δαπανάται για την αύξηση της εσωτερικής ενέργειας.
Η θερμοχωρητικότητα των αερίων σε σταθερή πίεση καθορίζεται από την ποσότητα θερμότητας που δαπανάται για την αύξηση της εσωτερικής ενέργειας.
Κατάσταση αερίου: χαρακτηριστικά, περιγραφή
Η θερμοχωρητικότητα ενός ιδανικού αερίου προσδιορίζεται λαμβάνοντας υπόψη το γεγονός ότι Сp-Сv=R. Η τελευταία ποσότητα ονομάζεται καθολική σταθερά αερίου. Η τιμή του αντιστοιχεί σε 8,314 J/(mol K).
Όταν πραγματοποιείτε θεωρητικούς υπολογισμούς της θερμοχωρητικότητας, για παράδειγμα, περιγράφοντας τη σχέση με τη θερμοκρασία, δεν αρκεί να χρησιμοποιείτε μόνο θερμοδυναμικές μεθόδους, είναι σημαντικό να οπλίζεστε με στοιχεία στατικής φυσικής.
Η θερμοχωρητικότητα των αερίων περιλαμβάνει τον υπολογισμό της μέσης τιμής της ενέργειας της μεταφορικής κίνησης ορισμένων μορίων. Αυτή η κίνηση συνοψίζεται από την περιστροφική και μεταφορική κίνηση του μορίου, καθώς και από τις εσωτερικές δονήσεις των ατόμων.
Στη στατική φυσική, υπάρχουν πληροφορίες ότι για κάθε βαθμό ελευθερίας περιστροφικής και μεταφορικής κίνησης, υπάρχει μια ποσότητα για ένα αέριο που ισούται με το ήμισυ της καθολικής σταθεράς αερίου.

Ενδιαφέροντα γεγονότα
Ένα σωματίδιο ενός μονοατομικού αερίου θεωρείται ότι έχει τρεις μεταφορικούς βαθμούς ελευθερίας, επομένως η ειδική θερμότητα ενός αερίου έχει τρεις μεταφορικούς, δύο περιστροφικούς και έναν δονητικούς βαθμούς ελευθερίας. Ο νόμος της ομοιόμορφης κατανομής τους οδηγεί στην εξίσωση της ειδικής θερμότητας σε σταθερό όγκο με R.
Κατά τη διάρκεια των πειραμάτων, διαπιστώθηκε ότι η θερμοχωρητικότητα ενός διατομικού αερίου αντιστοιχεί στην τιμή R. Μια τέτοια απόκλιση μεταξύ θεωρίας και πράξης εξηγείται από το γεγονός ότι η θερμοχωρητικότητα ενός ιδανικού αερίου σχετίζεται με το κβαντικό Επομένως, όταν κάνετε υπολογισμούς, είναι σημαντικό να χρησιμοποιείτε στατιστικά στοιχεία που βασίζονται σε κβαντικάμηχανική.
Με βάση τα θεμέλια της κβαντικής μηχανικής, οποιοδήποτε σύστημα σωματιδίων που ταλαντώνονται ή περιστρέφονται, συμπεριλαμβανομένων των μορίων αερίου, έχει μόνο ορισμένες διακριτές τιμές ενέργειας.
Αν η ενέργεια της θερμικής κίνησης στο σύστημα δεν είναι αρκετή για να διεγείρει ταλαντώσεις συγκεκριμένης συχνότητας, τέτοιες κινήσεις δεν συμβάλλουν στη συνολική θερμική ικανότητα του συστήματος.
Σαν αποτέλεσμα, ένας συγκεκριμένος βαθμός ελευθερίας γίνεται "παγωμένος", είναι αδύνατο να εφαρμοστεί ο νόμος της ισοκατανομής σε αυτόν.
Η θερμοχωρητικότητα των αερίων είναι ένα σημαντικό χαρακτηριστικό της κατάστασης από την οποία εξαρτάται η λειτουργία ολόκληρου του θερμοδυναμικού συστήματος.
Η θερμοκρασία στην οποία μπορεί να εφαρμοστεί ο νόμος της ισοκατανομής στον δονητικό ή περιστροφικό βαθμό ελευθερίας χαρακτηρίζεται από την κβαντική θεωρία, συνδέει τη σταθερά Planck με τη σταθερά Boltzmann.

Διατομικά αέρια
Τα κενά μεταξύ των επιπέδων περιστροφικής ενέργειας τέτοιων αερίων είναι ένας μικρός αριθμός μοιρών. Η εξαίρεση είναι το υδρογόνο, στο οποίο η τιμή της θερμοκρασίας καθορίζεται από εκατοντάδες βαθμούς.
Γι' αυτό η θερμοχωρητικότητα ενός αερίου σε σταθερή πίεση είναι δύσκολο να περιγραφεί με τον νόμο της ομοιόμορφης κατανομής. Στην κβαντική στατιστική, κατά τον προσδιορισμό της θερμοχωρητικότητας, λαμβάνεται υπόψη ότι το δονητικό τμήμα της, σε περίπτωση μείωσης της θερμοκρασίας, μειώνεται γρήγορα και φτάνει στο μηδέν.
Αυτό το φαινόμενο εξηγεί το γεγονός ότι σε θερμοκρασία δωματίου δεν υπάρχει σχεδόν κανένα δονητικό μέρος της θερμικής ικανότητας, γιαδιατομικό αέριο, αντιστοιχεί στη σταθερά R.
Η θερμοχωρητικότητα ενός αερίου σε σταθερό όγκο στην περίπτωση δεικτών χαμηλής θερμοκρασίας προσδιορίζεται με χρήση κβαντικών στατιστικών. Υπάρχει η αρχή Nernst, η οποία ονομάζεται τρίτος νόμος της θερμοδυναμικής. Με βάση τη σύνθεσή του, η μοριακή θερμοχωρητικότητα ενός αερίου θα μειώνεται με τη μείωση της θερμοκρασίας, τείνοντας στο μηδέν.

Χαρακτηριστικά στερεών
Αν η θερμοχωρητικότητα ενός μείγματος αερίων μπορεί να εξηγηθεί χρησιμοποιώντας κβαντικές στατιστικές, τότε για μια στερεή κατάσταση συσσωμάτωσης, η θερμική κίνηση χαρακτηρίζεται από ελαφρές διακυμάνσεις των σωματιδίων κοντά στη θέση ισορροπίας.
Κάθε άτομο έχει τρεις δονητικούς βαθμούς ελευθερίας, επομένως, σύμφωνα με τον νόμο ισοκατανομής, η γραμμομοριακή θερμοχωρητικότητα ενός στερεού μπορεί να υπολογιστεί ως 3nR, με το n να είναι ο αριθμός των ατόμων σε ένα μόριο.
Στην πράξη, αυτός ο αριθμός είναι το όριο στο οποίο τείνει η θερμική ικανότητα ενός στερεού σώματος σε υψηλές θερμοκρασίες.
Το μέγιστο μπορεί να επιτευχθεί σε συνηθισμένες θερμοκρασίες για ορισμένα στοιχεία, συμπεριλαμβανομένων των μετάλλων. Για n=1, ο νόμος Dulong και Petit πληρούται, αλλά για σύνθετες ουσίες είναι μάλλον δύσκολο να επιτευχθεί ένα τέτοιο όριο. Εφόσον το όριο δεν μπορεί να επιτευχθεί στην πραγματικότητα, συμβαίνει αποσύνθεση ή τήξη του στερεού.
Ιστορία της κβαντικής θεωρίας
Οι ιδρυτές της κβαντικής θεωρίας είναι ο Αϊνστάιν και ο Ντεμπίε στις αρχές του εικοστού αιώνα. Βασίζεται στην κβαντοποίηση των ταλαντωτικών κινήσεων των ατόμων σε ένα ορισμένοκρύσταλλο. Στην περίπτωση των δεικτών χαμηλής θερμοκρασίας, η θερμοχωρητικότητα ενός στερεού σώματος αποδεικνύεται ευθέως ανάλογη με την απόλυτη τιμή που λαμβάνεται σε κύβους. Αυτή η σχέση έχει ονομαστεί νόμος του Debye. Ως κριτήριο που καθιστά δυνατή τη διάκριση μεταξύ των δεικτών χαμηλής και υψηλής θερμοκρασίας, λαμβάνεται η σύγκρισή τους με τη θερμοκρασία Debye.
Αυτή η τιμή καθορίζεται από το φάσμα των δονήσεων ενός ατόμου στο σώμα, επομένως εξαρτάται σοβαρά από τα χαρακτηριστικά της κρυσταλλικής δομής του.
Το
QD είναι μια τιμή που έχει αρκετές εκατοντάδες K, αλλά, για παράδειγμα, είναι πολύ υψηλότερη στο διαμάντι.
Τα ηλεκτρόνια αγωγιμότητας συμβάλλουν σημαντικά στη θερμοχωρητικότητα των μετάλλων. Για τον υπολογισμό του χρησιμοποιούνται οι κβαντικές στατιστικές Fermi. Η ηλεκτρονική αγωγιμότητα για τα άτομα μετάλλου είναι ευθέως ανάλογη με την απόλυτη θερμοκρασία. Επειδή είναι ασήμαντη τιμή, λαμβάνεται υπόψη μόνο σε θερμοκρασίες που τείνουν στο απόλυτο μηδέν.
Μέθοδοι προσδιορισμού θερμοχωρητικότητας
Η κύρια πειραματική μέθοδος είναι η θερμιδομετρία. Για να πραγματοποιηθεί ένας θεωρητικός υπολογισμός της θερμοχωρητικότητας, χρησιμοποιείται στατιστική θερμοδυναμική. Ισχύει για ένα ιδανικό αέριο, καθώς και για κρυσταλλικά σώματα, πραγματοποιείται με βάση πειραματικά δεδομένα για τη δομή της ύλης.
Εμπειρικές μέθοδοι για τον υπολογισμό της θερμοχωρητικότητας ενός ιδανικού αερίου βασίζονται στην ιδέα της χημικής δομής, της συνεισφοράς μεμονωμένων ομάδων ατόμων στο Ср.
Για τα υγρά χρησιμοποιούνται επίσης μέθοδοι που βασίζονται στη χρήση θερμοδυναμικήςκύκλοι που καθιστούν δυνατή τη μετάβαση από τη θερμοχωρητικότητα ενός ιδανικού αερίου σε ένα υγρό μέσω του παραγώγου της θερμοκρασίας της ενθαλπίας της διαδικασίας εξάτμισης.
Στην περίπτωση διαλύματος, ο υπολογισμός της θερμοχωρητικότητας ως αθροιστική συνάρτηση δεν επιτρέπεται, καθώς η υπερβάλλουσα τιμή της θερμοχωρητικότητας του διαλύματος είναι βασικά σημαντική.
Για να το αξιολογήσουμε, χρειαζόμαστε τη μοριακή-στατιστική θεωρία των λύσεων. Το πιο δύσκολο είναι ο προσδιορισμός της θερμοχωρητικότητας των ετερογενών συστημάτων στη θερμοδυναμική ανάλυση.

Συμπέρασμα
Η μελέτη της θερμοχωρητικότητας σάς επιτρέπει να υπολογίσετε το ενεργειακό ισοζύγιο διεργασιών που λαμβάνουν χώρα σε χημικούς αντιδραστήρες, καθώς και σε άλλες συσκευές παραγωγής χημικών. Επιπλέον, αυτή η τιμή είναι απαραίτητη για την επιλογή των βέλτιστων τύπων ψυκτικών.
Προς το παρόν, ο πειραματικός προσδιορισμός της θερμοχωρητικότητας ουσιών για διάφορα διαστήματα θερμοκρασίας - από χαμηλές τιμές έως υψηλές τιμές - είναι η κύρια επιλογή για τον προσδιορισμό των θερμοδυναμικών χαρακτηριστικών μιας ουσίας. Κατά τον υπολογισμό της εντροπίας και της ενθαλπίας μιας ουσίας, χρησιμοποιούνται ολοκληρώματα θερμοχωρητικότητας. Οι πληροφορίες σχετικά με τη θερμική ικανότητα των χημικών αντιδραστηρίων σε ένα συγκεκριμένο εύρος θερμοκρασίας σάς επιτρέπουν να υπολογίσετε τη θερμική επίδραση της διαδικασίας. Οι πληροφορίες για τη θερμοχωρητικότητα των διαλυμάτων καθιστούν δυνατό τον υπολογισμό των θερμοδυναμικών παραμέτρων τους σε οποιεσδήποτε τιμές θερμοκρασίας εντός του αναλυόμενου διαστήματος.
Για παράδειγμα, ένα υγρό χαρακτηρίζεται από τη δαπάνη μέρους της θερμότητας για την αλλαγή της τιμής της δυνητικής ενέργειαςαντιδρώντα μόρια. Αυτή η τιμή ονομάζεται θερμοχωρητικότητα "διαμόρφωσης", που χρησιμοποιείται για την περιγραφή λύσεων.
Είναι δύσκολο να διεξαχθούν πλήρεις μαθηματικοί υπολογισμοί χωρίς να ληφθούν υπόψη τα θερμοδυναμικά χαρακτηριστικά μιας ουσίας, η κατάσταση συσσώρευσής της. Γι' αυτό για υγρά, αέρια, στερεά χρησιμοποιείται ένα χαρακτηριστικό όπως η ειδική θερμοχωρητικότητα, που καθιστά δυνατό τον χαρακτηρισμό των ενεργειακών παραμέτρων μιας ουσίας.






