Στη θερμοδυναμική, όταν μελετάμε τις μεταβάσεις από την αρχική στην τελική κατάσταση ενός συστήματος, είναι σημαντικό να γνωρίζουμε τη θερμική επίδραση της διαδικασίας. Η έννοια της θερμοχωρητικότητας συνδέεται στενά με αυτό το φαινόμενο. Σε αυτό το άρθρο, θα εξετάσουμε το ερώτημα του τι σημαίνει η ισοχορική θερμοχωρητικότητα ενός αερίου.
Ιδανικό αέριο
Ιδανικό αέριο είναι ένα αέριο του οποίου τα σωματίδια θεωρούνται υλικά σημεία, δηλαδή δεν έχουν διαστάσεις, αλλά έχουν μάζα και στο οποίο όλη η εσωτερική ενέργεια αποτελείται αποκλειστικά από την κινητική ενέργεια της κίνησης των μορίων και άτομα.
Οποιοδήποτε πραγματικό αέριο ιδανικά δεν θα ικανοποιήσει ποτέ το περιγραφόμενο μοντέλο, καθώς τα σωματίδια του εξακολουθούν να έχουν κάποιες γραμμικές διαστάσεις και αλληλεπιδρούν μεταξύ τους χρησιμοποιώντας ασθενείς δεσμούς van der Waals ή χημικούς δεσμούς άλλου τύπου. Ωστόσο, σε χαμηλές πιέσεις και υψηλές θερμοκρασίες, οι αποστάσεις μεταξύ των μορίων είναι μεγάλες και η κινητική τους ενέργεια υπερβαίνει τη δυναμική ενέργεια κατά δεκάδες φορές. Όλα αυτά καθιστούν δυνατή την εφαρμογή με υψηλό βαθμό ακρίβειας του ιδανικού μοντέλου για πραγματικά αέρια.
Εσωτερική ενέργεια αερίου
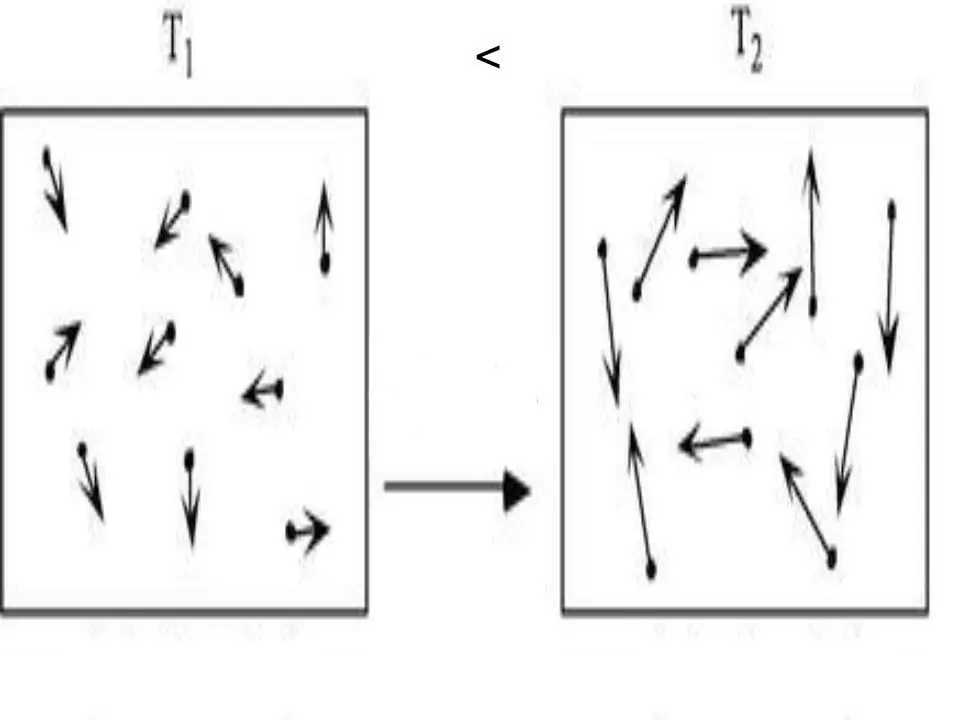
Η εσωτερική ενέργεια οποιουδήποτε συστήματος είναι ένα φυσικό χαρακτηριστικό, το οποίο ισούται με το άθροισμα του δυναμικού και της κινητικής ενέργειας. Εφόσον η δυναμική ενέργεια μπορεί να παραμεληθεί στα ιδανικά αέρια, μπορούμε να γράψουμε την ισότητα για αυτά:
U=Ek.
Όπου Ek είναι η ενέργεια του κινητικού συστήματος. Χρησιμοποιώντας τη μοριακή κινητική θεωρία και εφαρμόζοντας την καθολική εξίσωση κατάστασης Clapeyron-Mendeleev, δεν είναι δύσκολο να ληφθεί μια έκφραση για το U. Γράφεται παρακάτω:
U=z/2nRT.
Εδώ T, R και n είναι η απόλυτη θερμοκρασία, η σταθερά του αερίου και η ποσότητα της ουσίας, αντίστοιχα. Η τιμή z είναι ένας ακέραιος αριθμός που δείχνει τον αριθμό των βαθμών ελευθερίας που έχει ένα μόριο αερίου.
Ισοβαρική και ισοχωρική θερμοχωρητικότητα
Στη φυσική, η θερμοχωρητικότητα είναι η ποσότητα θερμότητας που πρέπει να παρέχεται στο υπό μελέτη σύστημα προκειμένου να θερμανθεί κατά ένα Κέλβιν. Ο αντίστροφος ορισμός ισχύει επίσης, δηλαδή, η θερμοχωρητικότητα είναι η ποσότητα θερμότητας που απελευθερώνει το σύστημα όταν ψύχεται κατά ένα Kelvin.
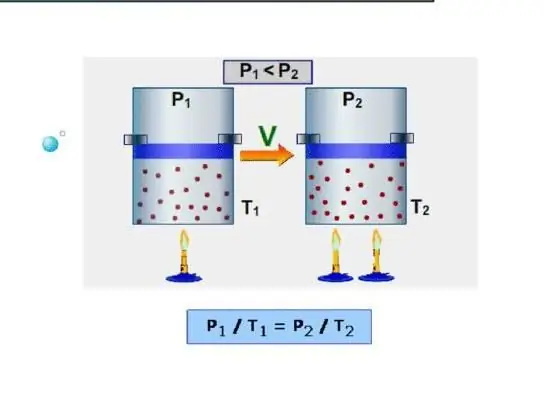
Ο ευκολότερος τρόπος για ένα σύστημα είναι να προσδιορίσει την ισοχωρική θερμοχωρητικότητα. Εννοείται ως η θερμοχωρητικότητα σε σταθερό όγκο. Δεδομένου ότι το σύστημα δεν εκτελεί εργασίες υπό τέτοιες συνθήκες, όλη η ενέργεια δαπανάται για την αύξηση των εσωτερικών ενεργειακών αποθεμάτων. Ας υποδηλώσουμε την ισοχορική θερμοχωρητικότητα με το σύμβολο CV, τότε μπορούμε να γράψουμε:
dU=CVdT.
Δηλαδή η αλλαγή στην εσωτερική ενέργειασύστημα είναι ευθέως ανάλογο με τη μεταβολή της θερμοκρασίας του. Εάν συγκρίνουμε αυτήν την έκφραση με την ισότητα που γράφτηκε στην προηγούμενη παράγραφο, τότε καταλήγουμε στον τύπο για το CV σε ένα ιδανικό αέριο:
СV=z/2nR.
Αυτή η τιμή δεν είναι βολική για χρήση στην πράξη, καθώς εξαρτάται από την ποσότητα της ουσίας στο σύστημα. Ως εκ τούτου, εισήχθη η έννοια της ειδικής ισοχωρικής θερμοχωρητικότητας, δηλαδή μια τιμή που υπολογίζεται είτε ανά 1 mol αερίου είτε ανά 1 kg. Ας υποδηλώσουμε την πρώτη τιμή με το σύμβολο CV, τη δεύτερη - με το σύμβολο CV m. Για αυτούς, μπορείτε να γράψετε τους ακόλουθους τύπους:
CV=z/2R;
CVm=z/2R/M.
Εδώ M είναι η μοριακή μάζα.
Ισοβαρική είναι η θερμοχωρητικότητα ενώ διατηρείται σταθερή η πίεση στο σύστημα. Ένα παράδειγμα τέτοιας διαδικασίας είναι η διαστολή αερίου σε έναν κύλινδρο κάτω από ένα έμβολο όταν θερμαίνεται. Σε αντίθεση με την ισοχωρική διαδικασία, κατά την ισοβαρική διεργασία, η θερμότητα που παρέχεται στο σύστημα δαπανάται για την αύξηση της εσωτερικής ενέργειας και για την εκτέλεση μηχανικών εργασιών, δηλαδή:
H=dU + PdV.
Η ενθαλπία μιας ισοβαρικής διεργασίας είναι το γινόμενο της ισοβαρικής θερμοχωρητικότητας και της μεταβολής της θερμοκρασίας στο σύστημα, δηλαδή:
H=CPdT.
Αν θεωρήσουμε τη διαστολή σε σταθερή πίεση 1 mol αερίου, τότε ο πρώτος νόμος της θερμοδυναμικής θα γραφτεί ως:
CPdT=CV dT + RdT.
Ο τελευταίος όρος προκύπτει από την εξίσωσηClapeyron-Mendeleev. Από αυτή την ισότητα προκύπτει η σχέση μεταξύ ισοβαρικής και ισοχορικής θερμικής ικανότητας:
CP=CV + R.
Για ένα ιδανικό αέριο, η ειδική μοριακή θερμοχωρητικότητα σε σταθερή πίεση είναι πάντα μεγαλύτερη από το αντίστοιχο ισοχορικό χαρακτηριστικό κατά R=8, 314 J/(molK).
Βαθμοί ελευθερίας μορίων και θερμοχωρητικότητα
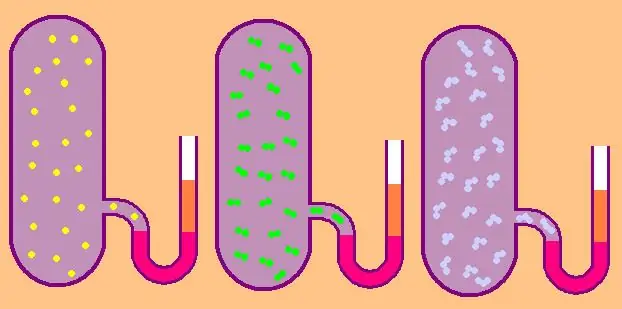
Ας γράψουμε ξανά τον τύπο για τη συγκεκριμένη μοριακή ισοχωρική θερμοχωρητικότητα:
CV=z/2R.
Στην περίπτωση ενός μονοατομικού αερίου, η τιμή z=3, καθώς τα άτομα στο διάστημα μπορούν να κινηθούν μόνο προς τρεις ανεξάρτητες κατευθύνσεις.
Αν μιλάμε για ένα αέριο που αποτελείται από διατομικά μόρια, για παράδειγμα, οξυγόνο O2 ή υδρογόνο H2, τότε, εκτός από τη μεταγραφική κίνηση, αυτά τα μόρια μπορούν ακόμα να περιστρέφονται γύρω από δύο αμοιβαία κάθετους άξονες, δηλαδή, το z θα είναι ίσο με 5.
Για πιο πολύπλοκα μόρια, χρησιμοποιήστε z=6. για να προσδιορίσετε CV






