Τα φυσικά φαινόμενα και διεργασίες γύρω μας είναι αρκετά περίπλοκα. Για την ακριβή φυσική τους περιγραφή, θα πρέπει να χρησιμοποιηθεί μια δυσκίνητη μαθηματική συσκευή και θα πρέπει να ληφθεί υπόψη ένας μεγάλος αριθμός σημαντικών παραγόντων. Για να αποφευχθεί αυτό το πρόβλημα, χρησιμοποιούνται ορισμένα απλουστευμένα μοντέλα στη φυσική, τα οποία διευκολύνουν πολύ τη μαθηματική ανάλυση της διαδικασίας, αλλά πρακτικά δεν επηρεάζουν την ακρίβεια της περιγραφής της. Ένα από αυτά είναι το ιδανικό μοντέλο αερίου. Ας το εξετάσουμε πιο αναλυτικά στο άρθρο.
Η ιδέα ενός ιδανικού αερίου
Ιδανικό αέριο είναι η κατάσταση συσσωμάτωσης μιας ουσίας, η οποία αποτελείται από υλικά σημεία που δεν αλληλεπιδρούν μεταξύ τους. Ας εξηγήσουμε αυτόν τον ορισμό με περισσότερες λεπτομέρειες.
Πρώτον, μιλάμε για υλικά σημεία ως αντικείμενα που συνθέτουν ένα ιδανικό αέριο. Αυτό σημαίνει ότι τα μόρια και τα άτομά του δεν έχουν μέγεθος, αλλά έχουν συγκεκριμένη μάζα. Είναι τολμηρόμπορεί να γίνει μια προσέγγιση λαμβάνοντας υπόψη το γεγονός ότι σε όλα τα πραγματικά αέρια σε χαμηλές πιέσεις και υψηλές θερμοκρασίες, η απόσταση μεταξύ των μορίων είναι πολύ μεγαλύτερη από τις γραμμικές τους διαστάσεις.
Δεύτερον, τα μόρια σε ένα ιδανικό αέριο δεν πρέπει να αλληλεπιδρούν μεταξύ τους. Στην πραγματικότητα, τέτοιες αλληλεπιδράσεις υπάρχουν πάντα. Έτσι, ακόμη και άτομα ευγενών αερίων βιώνουν έλξη διπόλου-διπόλου. Με άλλα λόγια, υπάρχουν αλληλεπιδράσεις van der Waals. Ωστόσο, σε σύγκριση με την κινητική ενέργεια της περιστροφής και της μεταφορικής κίνησης των μορίων, αυτές οι αλληλεπιδράσεις είναι τόσο μικρές που δεν επηρεάζουν τις ιδιότητες των αερίων. Επομένως, δεν μπορούν να ληφθούν υπόψη κατά την επίλυση πρακτικών προβλημάτων.
Είναι σημαντικό να σημειωθεί ότι δεν μπορούν να θεωρηθούν ιδανικά όλα τα αέρια στα οποία η πυκνότητα είναι χαμηλή και η θερμοκρασία υψηλή. Εκτός από τις αλληλεπιδράσεις van der Waals, υπάρχουν και άλλοι, ισχυρότεροι τύποι δεσμών, για παράδειγμα, δεσμοί υδρογόνου μεταξύ μορίων H2O, οι οποίοι οδηγούν σε κατάφωρη παραβίαση των συνθηκών ιδανικότητας αερίου. Για το λόγο αυτό, οι υδρατμοί δεν είναι ιδανικό αέριο, αλλά ο αέρας είναι.
Φυσικό μοντέλο ιδανικού αερίου
Αυτό το μοντέλο μπορεί να αναπαρασταθεί ως εξής: ας υποθέσουμε ότι το σύστημα αερίων περιέχει N σωματίδια. Αυτά μπορεί να είναι άτομα και μόρια διαφόρων χημικών ουσιών και στοιχείων. Ο αριθμός των σωματιδίων Ν είναι μεγάλος, επομένως η μονάδα "mole" χρησιμοποιείται συνήθως για την περιγραφή του (1 mole αντιστοιχεί στον αριθμό του Avogadro). Όλα κινούνται σε κάποιο όγκο V. Κινήσεις σωματιδίωνείναι χαοτικές και ανεξάρτητες μεταξύ τους. Καθένα από αυτά έχει μια συγκεκριμένη ταχύτητα v και κινείται κατά μήκος μιας ευθείας διαδρομής.
Θεωρητικά, η πιθανότητα σύγκρουσης μεταξύ των σωματιδίων είναι σχεδόν μηδενική, αφού το μέγεθός τους είναι μικρό σε σύγκριση με τις διασωματιδιακές αποστάσεις. Ωστόσο, εάν συμβεί μια τέτοια σύγκρουση, τότε είναι απολύτως ελαστική. Στην τελευταία περίπτωση, η συνολική ορμή των σωματιδίων και η κινητική τους ενέργεια διατηρούνται.
Το θεωρούμενο μοντέλο ιδανικών αερίων είναι ένα κλασικό σύστημα με τεράστιο αριθμό στοιχείων. Επομένως, η ταχύτητα και η ενέργεια των σωματιδίων σε αυτό υπακούουν στη στατιστική κατανομή του Maxwell-Boltzmann. Ορισμένα σωματίδια έχουν χαμηλές ταχύτητες, ενώ άλλα έχουν υψηλές ταχύτητες. Σε αυτή την περίπτωση, υπάρχει ένα συγκεκριμένο στενό όριο ταχύτητας, στο οποίο βρίσκονται οι πιο πιθανές τιμές αυτής της ποσότητας. Η κατανομή ταχύτητας των μορίων αζώτου φαίνεται σχηματικά παρακάτω.
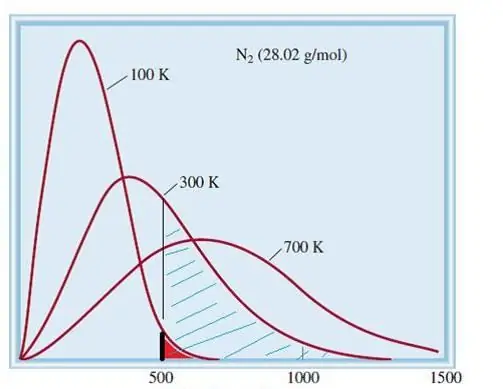
Κινητική θεωρία αερίων
Το μοντέλο των ιδανικών αερίων που περιγράφηκε παραπάνω καθορίζει μοναδικά τις ιδιότητες των αερίων. Αυτό το μοντέλο προτάθηκε για πρώτη φορά από τον Daniel Bernoulli το 1738.

Στη συνέχεια, αναπτύχθηκε στη σημερινή του κατάσταση από τους August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski και άλλους επιστήμονες.
Η κινητική θεωρία των ρευστών ουσιών, βάσει της οποίας χτίζεται το μοντέλο ιδανικού αερίου, εξηγεί δύο σημαντικές μακροσκοπικές ιδιότητες του συστήματος με βάση τη μικροσκοπική συμπεριφορά του:
- Η πίεση στα αέρια είναι το αποτέλεσμα της σύγκρουσης σωματιδίων με τα τοιχώματα του δοχείου.
- Η θερμοκρασία στο σύστημα είναι το αποτέλεσμα της εκδήλωσης της συνεχούς κίνησης των μορίων και των ατόμων.
Ας επεκταθούμε και στα δύο συμπεράσματα της κινητικής θεωρίας.
Πίεση αερίου
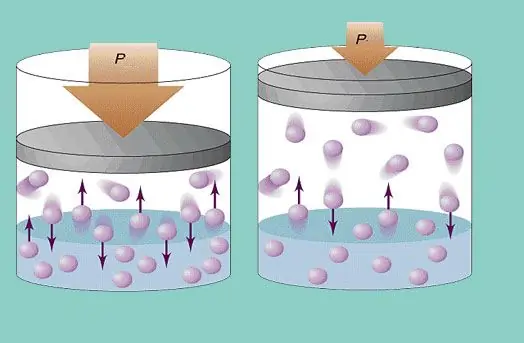
Το μοντέλο ιδανικού αερίου προϋποθέτει μια συνεχή χαοτική κίνηση των σωματιδίων στο σύστημα και τη συνεχή σύγκρουσή τους με τα τοιχώματα του σκάφους. Κάθε τέτοια σύγκρουση θεωρείται απολύτως ελαστική. Η μάζα των σωματιδίων είναι μικρή (≈10-27-10-25 kg). Επομένως, δεν μπορεί να δημιουργήσει μεγάλη πίεση σε μια σύγκρουση. Ωστόσο, ο αριθμός των σωματιδίων, και επομένως ο αριθμός των συγκρούσεων, είναι τεράστιος (≈1023). Επιπλέον, η μέση τετραγωνική ταχύτητα ρίζας των στοιχείων είναι αρκετές εκατοντάδες μέτρα ανά δευτερόλεπτο σε θερμοκρασία δωματίου. Όλα αυτά οδηγούν στη δημιουργία αισθητής πίεσης στα τοιχώματα του αγγείου. Μπορεί να υπολογιστεί χρησιμοποιώντας τον ακόλουθο τύπο:
P=Nmvcp2 / (3V), όπου vcp είναι ρίζα μέση τετραγωνική ταχύτητα, m είναι μάζα σωματιδίων.
Απόλυτη θερμοκρασία
Σύμφωνα με το μοντέλο ιδανικού αερίου, η θερμοκρασία καθορίζεται μοναδικά από τη μέση κινητική ενέργεια ενός μορίου ή ατόμου στο υπό μελέτη σύστημα. Μπορείτε να γράψετε την ακόλουθη έκφραση που συσχετίζει την κινητική ενέργεια και την απόλυτη θερμοκρασία για ένα ιδανικό αέριο:
mvcp2 / 2=3 / 2kB T.
Εδώ kB είναι η σταθερά Boltzmann. Από αυτήν την ισότητα παίρνουμε:
T=m vcp2 / (3kB).
Καθολική εξίσωση κατάστασης
Αν συνδυάσουμε τις παραπάνω εκφράσεις για απόλυτη πίεση P και απόλυτη θερμοκρασία T, μπορούμε να γράψουμε την ακόλουθη ισότητα:
PV=nRT.
Εδώ n είναι η ποσότητα της ουσίας σε mol, R είναι η σταθερά αερίου που εισήγαγε ο D. I. Mendeleev. Αυτή η έκφραση είναι η πιο σημαντική εξίσωση στη θεωρία των ιδανικών αερίων, γιατί συνδυάζει τρεις θερμοδυναμικές παραμέτρους (V, P, T) και δεν εξαρτάται από τα χημικά χαρακτηριστικά του συστήματος αερίων.

Η καθολική εξίσωση προέκυψε για πρώτη φορά πειραματικά από τον Γάλλο φυσικό Emile Clapeyron τον 19ο αιώνα και στη συνέχεια έφερε στη σύγχρονη μορφή της από τον Ρώσο χημικό Mendeleev, γι' αυτό και σήμερα φέρει τα ονόματα αυτών των επιστημόνων.






