Ιδανικό αέριο, η εξίσωση κατάστασης του ιδανικού αερίου, η θερμοκρασία και η πίεσή του, ο όγκος… ο κατάλογος των παραμέτρων και των ορισμών που χρησιμοποιούνται στην αντίστοιχη ενότητα της φυσικής μπορεί να συνεχιστεί για αρκετό καιρό. Σήμερα θα μιλήσουμε μόνο για αυτό το θέμα.
Τι θεωρείται στη μοριακή φυσική;

Το κύριο αντικείμενο που εξετάζεται σε αυτήν την ενότητα είναι ένα ιδανικό αέριο. Η ιδανική εξίσωση κατάστασης αερίου λήφθηκε λαμβάνοντας υπόψη τις κανονικές περιβαλλοντικές συνθήκες και θα μιλήσουμε για αυτό λίγο αργότερα. Τώρα ας προσεγγίσουμε αυτό το «πρόβλημα» από μακριά.
Ας υποθέσουμε ότι έχουμε κάποια μάζα αερίου. Η κατάστασή του μπορεί να προσδιοριστεί χρησιμοποιώντας τρεις παραμέτρους θερμοδυναμικής φύσης. Αυτά είναι φυσικά η πίεση, ο όγκος και η θερμοκρασία. Η εξίσωση της κατάστασης του συστήματος σε αυτή την περίπτωση θα είναι ο τύπος για τη σχέση μεταξύ των αντίστοιχων παραμέτρων. Μοιάζει με αυτό: F (p, V, T)=0.
Εδώ, για πρώτη φορά, πλησιάζουμε σιγά σιγά στην ανάδυση ενός τέτοιου πράγματος ως ιδανικόαέριο. Ονομάζεται αέριο στο οποίο οι αλληλεπιδράσεις μεταξύ των μορίων είναι αμελητέες. Γενικά, αυτό δεν υπάρχει στη φύση. Ωστόσο, οποιοδήποτε εξαιρετικά σπάνιο αέριο είναι κοντά σε αυτό. Το άζωτο, το οξυγόνο και ο αέρας, που βρίσκονται υπό κανονικές συνθήκες, διαφέρουν ελάχιστα από το ιδανικό. Για να γράψουμε την εξίσωση κατάστασης για ένα ιδανικό αέριο, μπορούμε να χρησιμοποιήσουμε τον ενιαίο νόμο αερίων. Παίρνουμε: pV/T=const.
Σχετική έννοια 1: Νόμος του Avogadro
Μπορεί να μας πει ότι αν πάρουμε τον ίδιο αριθμό γραμμομορίων οποιουδήποτε απολύτως τυχαίου αερίου και τα βάλουμε στις ίδιες συνθήκες, συμπεριλαμβανομένης της θερμοκρασίας και της πίεσης, τότε τα αέρια θα καταλάβουν τον ίδιο όγκο. Συγκεκριμένα, το πείραμα πραγματοποιήθηκε υπό κανονικές συνθήκες. Αυτό σημαίνει ότι η θερμοκρασία ήταν 273,15 Kelvin, η πίεση ήταν μία ατμόσφαιρα (760 χιλιοστά υδραργύρου ή 101325 Pascals). Με αυτές τις παραμέτρους, το αέριο καταλάμβανε όγκο ίσο με 22,4 λίτρα. Επομένως, μπορούμε να πούμε ότι για ένα γραμμομόριο οποιουδήποτε αερίου, ο λόγος των αριθμητικών παραμέτρων θα είναι μια σταθερή τιμή. Αυτός είναι ο λόγος για τον οποίο αποφασίστηκε να χαρακτηριστεί αυτό το σχήμα με το γράμμα R και να το ονομάσουμε καθολική σταθερά αερίου. Έτσι, ισούται με 8,31. Η μονάδα είναι J/molK.
Ιδανικό αέριο. Η εξίσωση της κατάστασης του ιδανικού αερίου και ο χειρισμός της
Ας προσπαθήσουμε να ξαναγράψουμε τον τύπο. Για να γίνει αυτό, το γράφουμε με αυτή τη μορφή: pV=RT. Στη συνέχεια, εκτελούμε μια απλή ενέργεια, πολλαπλασιάζουμε και τις δύο πλευρές της εξίσωσης με έναν αυθαίρετο αριθμό mol. Παίρνουμε pVu=uRT. Ας λάβουμε υπόψη το γεγονός ότι το γινόμενο του μοριακού όγκου καιη ποσότητα της ύλης είναι απλώς ο όγκος. Αλλά τελικά, ο αριθμός των γραμμομορίων θα είναι ταυτόχρονα ίσος με το πηλίκο της μάζας και της μοριακής μάζας. Έτσι ακριβώς μοιάζει η εξίσωση Mendeleev-Clapeyron. Δίνει μια σαφή ιδέα για το τι είδους σύστημα σχηματίζει ένα ιδανικό αέριο. Η εξίσωση κατάστασης για ένα ιδανικό αέριο θα έχει τη μορφή: pV=mRT/M.
Συναγώγετε τον τύπο για την πίεση
Ας κάνουμε μερικούς ακόμα χειρισμούς με τις εκφράσεις που ελήφθησαν. Για να γίνει αυτό, η δεξιά πλευρά της εξίσωσης Mendeleev-Clapeyron πολλαπλασιάζεται και διαιρείται με τον αριθμό Avogadro. Τώρα εξετάζουμε προσεκτικά το γινόμενο της ποσότητας της ουσίας με τον αριθμό Avogadro. Αυτό δεν είναι παρά ο συνολικός αριθμός μορίων στο αέριο. Αλλά ταυτόχρονα, ο λόγος της καθολικής σταθεράς του αερίου προς τον αριθμό Avogadro θα είναι ίσος με τη σταθερά Boltzmann. Επομένως, οι τύποι για την πίεση μπορούν να γραφτούν ως εξής: p=NkT/V ή p=nkT. Εδώ το σύμβολο n είναι η συγκέντρωση σωματιδίων.
Ιδανικές διεργασίες αερίου
Στη μοριακή φυσική υπάρχει κάτι σαν ισοδιεργασίες. Πρόκειται για θερμοδυναμικές διεργασίες που λαμβάνουν χώρα στο σύστημα σε μία από τις σταθερές παραμέτρους. Σε αυτή την περίπτωση, η μάζα της ουσίας πρέπει επίσης να παραμείνει σταθερή. Ας τα δούμε πιο συγκεκριμένα. Έτσι, οι νόμοι ενός ιδανικού αερίου.
Η πίεση παραμένει σταθερή
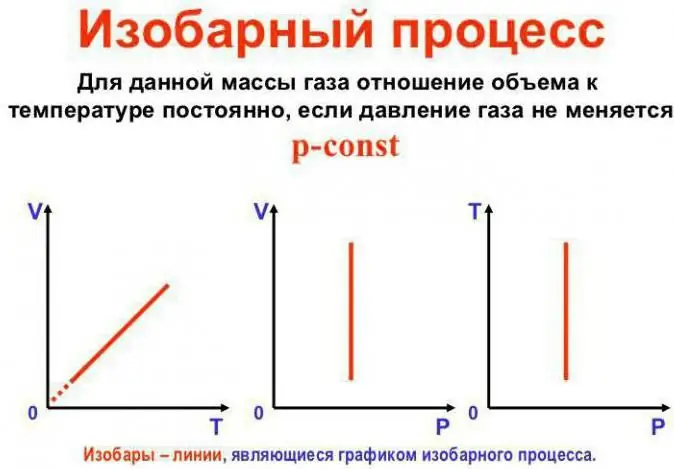
Αυτός είναι ο νόμος του Gay-Lussac. Μοιάζει με αυτό: V/T=const. Μπορεί να ξαναγραφτεί με άλλο τρόπο: V=Vo (1 + at). Εδώ το a ισούται με 1/273,15 K^-1 και ονομάζεται «συντελεστής επέκτασης όγκου». Μπορούμε να αντικαταστήσουμε τη θερμοκρασία τόσο σε Κελσίου όσο και σετην κλίμακα Kelvin. Στην τελευταία περίπτωση, παίρνουμε τον τύπο V=Voat.
Η ένταση παραμένει σταθερή

Αυτός είναι ο δεύτερος νόμος του Gay-Lussac, ο οποίος αναφέρεται πιο συχνά ως νόμος του Καρόλου. Μοιάζει με αυτό: p/T=const. Υπάρχει μια άλλη διατύπωση: p=po (1 + at). Οι μετασχηματισμοί μπορούν να πραγματοποιηθούν σύμφωνα με το προηγούμενο παράδειγμα. Όπως μπορείτε να δείτε, οι νόμοι του ιδανικού αερίου μερικές φορές μοιάζουν αρκετά μεταξύ τους.
Η θερμοκρασία παραμένει σταθερή

Αν η θερμοκρασία ενός ιδανικού αερίου παραμένει σταθερή, τότε μπορούμε να πάρουμε τον νόμο Boyle-Mariotte. Μπορεί να γραφτεί ως εξής: pV=const.
Σχετική έννοια 2: Μερική πίεση
Ας πούμε ότι έχουμε ένα δοχείο με αέρια. Θα είναι ένα μείγμα. Το σύστημα βρίσκεται σε κατάσταση θερμικής ισορροπίας και τα ίδια τα αέρια δεν αντιδρούν μεταξύ τους. Εδώ το Ν θα υποδηλώνει τον συνολικό αριθμό των μορίων. N1, N2 και ούτω καθεξής, αντίστοιχα, ο αριθμός των μορίων σε καθένα από τα συστατικά του μείγματος. Ας πάρουμε τον τύπο πίεσης p=nkT=NkT/V. Μπορεί να ανοίξει για μια συγκεκριμένη περίπτωση. Για ένα μείγμα δύο συστατικών, ο τύπος θα έχει τη μορφή: p=(N1 + N2) kT/V. Αλλά τότε αποδεικνύεται ότι η συνολική πίεση θα αθροιστεί από τις μερικές πιέσεις κάθε μείγματος. Έτσι, θα μοιάζει με p1 + p2 και ούτω καθεξής. Αυτές θα είναι οι μερικές πιέσεις.
Γιατί είναι;
Ο τύπος που λάβαμε δείχνει ότι η πίεση στο σύστημα προέρχεται από κάθε ομάδα μορίων. Παρεμπιπτόντως, δεν εξαρτάται απόοι υπολοιποι. Ο Ντάλτον το εκμεταλλεύτηκε αυτό κατά τη διατύπωση του νόμου, ο οποίος αργότερα πήρε το όνομά του: σε ένα μείγμα όπου τα αέρια δεν αντιδρούν χημικά μεταξύ τους, η συνολική πίεση θα είναι ίση με το άθροισμα των μερικών πιέσεων.






