Τα αέρια, από την άποψη της θερμοδυναμικής, περιγράφονται από ένα σύνολο μακροσκοπικών χαρακτηριστικών, τα κυριότερα από τα οποία είναι η θερμοκρασία, η πίεση και ο όγκος. Η σταθερότητα μιας από αυτές τις παραμέτρους και η αλλαγή στις άλλες δύο υποδηλώνει ότι μια ή άλλη ισοδιεργασία συμβαίνει στο αέριο. Θα αφιερώσουμε αυτό το άρθρο σε μια λεπτομερή απάντηση στα ερωτήματα ότι αυτή είναι μια ισοχορική διαδικασία, πώς διαφέρει από τις ισοθερμικές και ισοβαρικές αλλαγές στις καταστάσεις ενός συστήματος αερίων.
Ιδανικό αέριο στη φυσική

Πριν απαντήσετε στην ερώτηση ότι αυτή είναι μια ισοχορική διαδικασία, θα πρέπει να γνωρίσετε καλύτερα την έννοια του ιδανικού αερίου. Στη φυσική, νοείται κάθε αέριο στο οποίο η μέση κινητική ενέργεια των σωματιδίων που το αποτελούν υπερβαίνει κατά πολύ τη δυναμική ενέργεια της αλληλεπίδρασής τους και οι αποστάσεις μεταξύ αυτών των σωματιδίων είναι αρκετές τάξεις μεγέθους μεγαλύτερες από τις γραμμικές τους διαστάσεις. Υπό τις σημειωθείσες συνθήκες, είναι δυνατό, κατά την εκτέλεσηοι υπολογισμοί δεν λαμβάνουν υπόψη την ενέργεια αλληλεπίδρασης μεταξύ των σωματιδίων (είναι ίση με μηδέν), και μπορεί επίσης να υποτεθεί ότι τα σωματίδια είναι υλικά σημεία με μια ορισμένη μάζα m.
Η μόνη διαδικασία που λαμβάνει χώρα σε ένα ιδανικό αέριο είναι η σύγκρουση σωματιδίων με τα τοιχώματα του δοχείου που περιέχει την ουσία. Αυτές οι συγκρούσεις εκδηλώνονται στην πράξη ως ύπαρξη ορισμένης πίεσης στο αέριο P.
Κατά κανόνα, κάθε αέρια ουσία που αποτελείται από σχετικά χημικά αδρανή μόρια και έχει χαμηλή πίεση και υψηλές θερμοκρασίες μπορεί να θεωρηθεί ιδανικό αέριο με επαρκή ακρίβεια για πρακτικούς υπολογισμούς.
Εξίσωση που περιγράφει ένα ιδανικό αέριο
Φυσικά, μιλάμε για τον καθολικό νόμο του Clapeyron-Mendeleev, ο οποίος θα πρέπει να γίνει καλά κατανοητός για να καταλάβουμε ότι πρόκειται για μια ισοχορική διαδικασία. Έτσι, η καθολική εξίσωση κατάστασης έχει την ακόλουθη μορφή:
PV=nRT.
Δηλαδή, το γινόμενο της πίεσης P και του όγκου του αερίου V είναι ίσο με το γινόμενο της απόλυτης θερμοκρασίας T και της ποσότητας της ουσίας σε moles n, όπου R είναι ο παράγοντας αναλογικότητας. Η ίδια η εξίσωση γράφτηκε για πρώτη φορά από τον Emile Clapeyron το 1834 και στη δεκαετία του '70 του 19ου αιώνα, ο D. Mendeleev αντικατέστησε σε αυτήν ένα σύνολο σταθερών τιμών μιας καθολικής σταθεράς αερίου R (8,314 J/(molK)).
Σύμφωνα με την εξίσωση Clapeyron-Mendeleev, σε ένα κλειστό σύστημα ο αριθμός των σωματιδίων αερίου παραμένει σταθερός, επομένως υπάρχουν μόνο τρεις μακροσκοπικές παράμετροι που μπορούν να αλλάξουν (T, Pκαι V). Το τελευταίο γεγονός αποτελεί τη βάση της κατανόησης των διαφόρων ισοδιαδικασιών που θα συζητηθούν παρακάτω.
Τι είναι η ισοχορική διαδικασία;
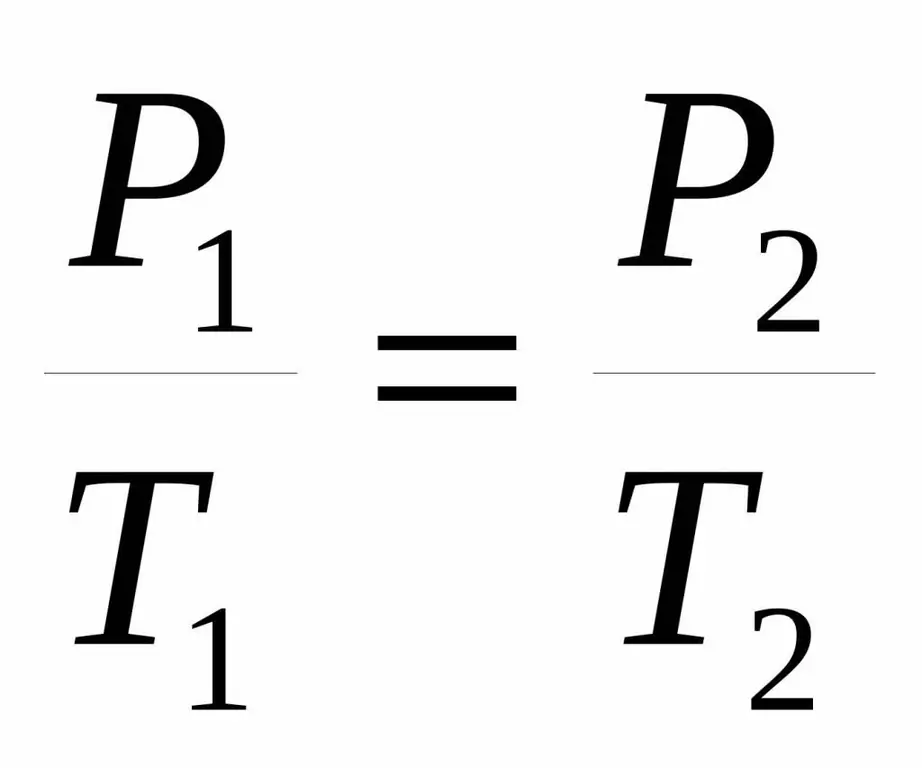
Αυτή η διαδικασία νοείται ως απολύτως οποιαδήποτε αλλαγή στην κατάσταση του συστήματος, στην οποία διατηρείται ο όγκος του.
Αν στραφούμε στην καθολική εξίσωση κατάστασης, μπορούμε να πούμε ότι σε μια ισοχορική διαδικασία μόνο η πίεση και η απόλυτη θερμοκρασία αλλάζουν σε ένα αέριο. Για να κατανοήσουμε ακριβώς πώς αλλάζουν οι θερμοδυναμικές παράμετροι, γράφουμε την αντίστοιχη μαθηματική παράσταση:
P / T=συνεχ.
Μερικές φορές αυτή η ισότητα δίνεται με ελαφρώς διαφορετική μορφή:
P1 / T1=P2 / T 2.
Και οι δύο ισότητες ονομάζονται νόμος του Καρόλου από το όνομα ενός Γάλλου επιστήμονα, ο οποίος στα τέλη του 18ου αιώνα απέκτησε την αναφερόμενη εξάρτηση πειραματικά.

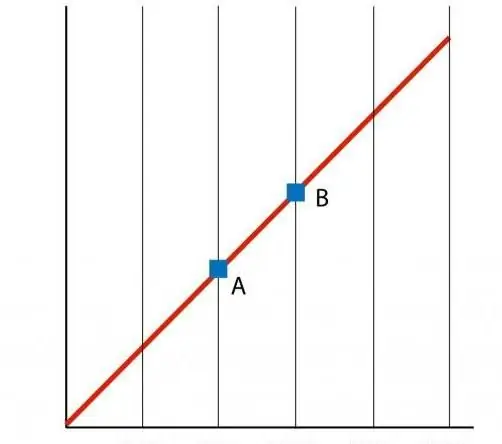
Αν οικοδομήσουμε ένα γράφημα της συνάρτησης P(T), τότε παίρνουμε μια ευθύγραμμη εξάρτηση, η οποία ονομάζεται ισόχωρη. Οποιαδήποτε ισόχωρη (για όλες τις τιμές των n και V) είναι μια ευθεία γραμμή.
Ενεργειακή περιγραφή της διαδικασίας
Όπως σημειώθηκε, μια ισοχορική διαδικασία είναι μια αλλαγή στην κατάσταση ενός συστήματος που λαμβάνει χώρα σε ένα κλειστό αλλά όχι απομονωμένο σύστημα. Μιλάμε για τη δυνατότητα ανταλλαγής θερμότητας μεταξύ του αερίου και του περιβάλλοντος. Γενικά, οποιαδήποτε παροχή θερμότητας Q στο σύστημα οδηγεί σε δύο αποτελέσματα:
- αλλάζει την εσωτερική ενέργεια U;
- αέριολειτουργεί Α, διαστέλλεται ή συστέλλεται.
Το τελευταίο συμπέρασμα γράφεται μαθηματικά ως εξής:
Q=U + A.
Η ισοχωρική διεργασία ενός ιδανικού αερίου, εξ ορισμού της, δεν συνεπάγεται εργασία που εκτελείται από το αέριο, αφού ο όγκος του παραμένει αμετάβλητος. Αυτό σημαίνει ότι όλη η θερμότητα που παρέχεται στο σύστημα πηγαίνει για να αυξήσει την εσωτερική του ενέργεια:
Q=U.
Αν αντικαταστήσουμε τον ρητό τύπο για την εσωτερική ενέργεια σε αυτήν την έκφραση, τότε η θερμότητα της ισοχωρικής διαδικασίας μπορεί να αναπαρασταθεί ως:
Q=z / 2nRT.
Εδώ z είναι ο αριθμός των βαθμών ελευθερίας, ο οποίος καθορίζεται από την πολυατομική φύση των μορίων που συνθέτουν το αέριο. Για ένα μονοατομικό αέριο, z=3, για ένα διατομικό αέριο - 5, και για ένα τριατομικό και περισσότερο - 6. Εδώ, κάτω από τους βαθμούς ελευθερίας, εννοούμε μεταφορικές και περιστροφικές μοίρες.
Αν συγκρίνουμε την απόδοση της θέρμανσης ενός συστήματος αερίου σε ισοχωρικές και ισοβαρικές διεργασίες, τότε στην πρώτη περίπτωση θα πάρουμε τη μέγιστη απόδοση, αφού κατά την ισοβαρή αλλαγή στην κατάσταση του συστήματος, το αέριο διαστέλλεται και μέρος της εισροής θερμότητας δαπανάται για την εκτέλεση εργασιών.
Ισοβαρική διεργασία
Παραπάνω περιγράψαμε λεπτομερώς ότι πρόκειται για μια ισοχορική διαδικασία. Ας πούμε τώρα λίγα λόγια για άλλες ισοδιεργασίες. Ας ξεκινήσουμε με το ισοβαρικό. Με βάση το όνομα, νοείται ως η μετάβαση του συστήματος μεταξύ καταστάσεων σε σταθερή πίεση. Αυτή η διαδικασία περιγράφεται από τον νόμο Gay-Lussac ως εξής:
V / T=συνεχ.
Όπως και με την ισοχώρη, η ισοbar V(T) αντιπροσωπεύει επίσης μια ευθεία γραμμή στο γράφημα.
Γιαοποιασδήποτε ισοβαρικής διεργασίας, είναι βολικό να υπολογιστεί το έργο που εκτελεί το αέριο, καθώς είναι ίσο με το γινόμενο της σταθερής πίεσης και της μεταβολής του όγκου.
Ισοθερμική διαδικασία
Αυτή είναι μια διαδικασία κατά την οποία η θερμοκρασία του συστήματος παραμένει σταθερή. Περιγράφεται από τον νόμο Boyle-Mariotte για ένα ιδανικό αέριο. Είναι περίεργο να σημειωθεί ότι αυτός είναι ο πρώτος πειραματικά ανακαλυφθείς νόμος αερίων (δεύτερο μισό του 17ου αιώνα). Η μαθηματική του σημειογραφία μοιάζει με αυτό:
PV=συνεχ.
Ισοχωρικές και ισοθερμικές διεργασίες διαφέρουν ως προς τη γραφική τους αναπαράσταση, καθώς η συνάρτηση P(V) είναι υπερβολική και όχι γραμμική σχέση.
Παράδειγμα επίλυσης προβλημάτων
Ας ενοποιήσουμε τις θεωρητικές πληροφορίες που παρέχονται στο άρθρο από την εφαρμογή τους για να λύσουμε ένα πρακτικό πρόβλημα. Είναι γνωστό ότι το καθαρό αέριο άζωτο βρισκόταν σε έναν κύλινδρο σε πίεση 1 ατμόσφαιρας και θερμοκρασία 25 °C. Αφού θερμάνθηκε ο κύλινδρος αερίου και μετρήθηκε η πίεση σε αυτόν, αποδείχθηκε ότι ήταν 1,5 ατμόσφαιρες. Ποια είναι η θερμοκρασία του αερίου στον κύλινδρο μετά τη θέρμανση; Κατά πόσο άλλαξε η εσωτερική ενέργεια του αερίου αν υπήρχαν 4 moles αζώτου στο μπαλόνι.
Για να απαντήσουμε στην πρώτη ερώτηση, χρησιμοποιούμε την ακόλουθη έκφραση:
P1 / T1=P2 / T 2.
Από πού παίρνουμε:
T2=P2 / P1 T 1.
Σε αυτήν την έκφραση, η πίεση μπορεί να αντικατασταθεί σε αυθαίρετες μονάδεςμετρήσεις, αφού συρρικνώνονται και η θερμοκρασία είναι μόνο σε Kelvin. Με αυτά τα λόγια, παίρνουμε:
T2=1,5 /1298,15=447,224 K.
Η υπολογιζόμενη θερμοκρασία σε βαθμούς Κελσίου είναι 174 °C.
Δεδομένου ότι το μόριο του αζώτου είναι διατομικό, η μεταβολή στην εσωτερική του ενέργεια κατά τη θέρμανση μπορεί να προσδιοριστεί ως εξής:
ΔU=5 / 2nRΔT.
Αντικαθιστώντας τις γνωστές τιμές σε αυτήν την έκφραση, θα λάβουμε την απάντηση στη δεύτερη ερώτηση του προβλήματος: ΔU=+12,4 kJ.






