Ένα σημαντικό τμήμα της θερμοδυναμικής είναι η μελέτη των μετασχηματισμών μεταξύ διαφορετικών φάσεων μιας ουσίας, καθώς αυτές οι διεργασίες συμβαίνουν στην πράξη και έχουν θεμελιώδη σημασία για την πρόβλεψη της συμπεριφοράς ενός συστήματος υπό ορισμένες συνθήκες. Αυτοί οι μετασχηματισμοί ονομάζονται μεταβάσεις φάσης, στις οποίες είναι αφιερωμένο το άρθρο.
Η έννοια μιας φάσης και ενός συστατικού συστήματος

Πριν προχωρήσουμε στην εξέταση των μεταπτώσεων φάσης στη φυσική, είναι απαραίτητο να ορίσουμε την έννοια της ίδιας της φάσης. Όπως είναι γνωστό από το μάθημα της γενικής φυσικής, υπάρχουν τρεις καταστάσεις της ύλης: αέρια, στερεά και υγρή. Σε ένα ειδικό τμήμα της επιστήμης - στη θερμοδυναμική - οι νόμοι διατυπώνονται για τις φάσεις της ύλης και όχι για τις καταστάσεις συσσώρευσής τους. Ως φάση νοείται ένας ορισμένος όγκος ύλης που έχει ομοιογενή δομή, χαρακτηρίζεται από συγκεκριμένες φυσικές και χημικές ιδιότητες και χωρίζεται από την υπόλοιπη ύλη με όρια, τα οποία ονομάζονται ενδιάμεση φάση.
Έτσι, η έννοια της "φάσης" φέρει πολύ πιο πρακτικά σημαντικές πληροφορίες σχετικά με τις ιδιότητεςύλη από την κατάσταση συσσώρευσής της. Για παράδειγμα, η στερεά κατάσταση ενός μετάλλου όπως ο σίδηρος μπορεί να είναι στις ακόλουθες φάσεις: χαμηλής θερμοκρασίας μαγνητικό σώμα-κεντρικό κυβικό (BCC), χαμηλής θερμοκρασίας μη μαγνητικό bcc, προσωποκεντρικό κυβικό (fcc) και υψηλή θερμοκρασία μη μαγνητική bcc.
Εκτός από την έννοια της «φάσης», οι νόμοι της θερμοδυναμικής χρησιμοποιούν επίσης τον όρο «συστατικά», που σημαίνει τον αριθμό των χημικών στοιχείων που συνθέτουν ένα συγκεκριμένο σύστημα. Αυτό σημαίνει ότι η φάση μπορεί να είναι είτε μονοσυστατική (1 χημικό στοιχείο) είτε πολλαπλών συστατικών (πολλά χημικά στοιχεία).
Θεώρημα Gibbs και ισορροπία μεταξύ φάσεων του συστήματος

Για να κατανοήσουμε τις μεταβάσεις φάσης, είναι απαραίτητο να γνωρίζουμε τις συνθήκες ισορροπίας μεταξύ τους. Αυτές οι συνθήκες μπορούν να ληφθούν μαθηματικά λύνοντας το σύστημα των εξισώσεων Gibbs για καθεμία από αυτές, υποθέτοντας ότι η κατάσταση ισορροπίας επιτυγχάνεται όταν η συνολική ενέργεια Gibbs του συστήματος που απομονώνεται από εξωτερική επίδραση παύει να αλλάζει.
Σαν αποτέλεσμα της επίλυσης του υποδεικνυόμενου συστήματος εξισώσεων, προκύπτουν συνθήκες για την ύπαρξη ισορροπίας μεταξύ πολλών φάσεων: ένα απομονωμένο σύστημα θα πάψει να εξελίσσεται μόνο όταν οι πιέσεις, τα χημικά δυναμικά κάθε συστατικού και οι θερμοκρασίες σε όλες τις φάσεις είναι ίσα μεταξύ τους.
Κανόνας φάσης Gibbs για ισορροπία

Ένα σύστημα που αποτελείται από πολλές φάσεις και συστατικά μπορεί να βρίσκεται σε ισορροπία όχι μόνουπό ορισμένες συνθήκες, για παράδειγμα, σε συγκεκριμένη θερμοκρασία και πίεση. Μερικές από τις μεταβλητές στο θεώρημα Gibbs για την ισορροπία μπορούν να αλλάξουν διατηρώντας ταυτόχρονα τον αριθμό των φάσεων και τον αριθμό των συστατικών που βρίσκονται σε αυτήν την ισορροπία. Ο αριθμός των μεταβλητών που μπορούν να αλλάξουν χωρίς να διαταραχθεί η ισορροπία στο σύστημα ονομάζεται αριθμός ελευθεριών αυτού του συστήματος.
Ο αριθμός των ελευθεριών l ενός συστήματος που αποτελείται από f φάσεις και k συνιστώσες καθορίζεται μοναδικά από τον κανόνα φάσης Gibbs. Αυτός ο κανόνας γράφεται μαθηματικά ως εξής: l + f=k + 2. Πώς να δουλέψετε με αυτόν τον κανόνα; Πολύ απλό. Για παράδειγμα, είναι γνωστό ότι το σύστημα αποτελείται από f=3 φάσεις ισορροπίας. Ποιος είναι ο ελάχιστος αριθμός στοιχείων που μπορεί να περιέχει ένα τέτοιο σύστημα; Μπορείτε να απαντήσετε στην ερώτηση συλλογίζοντας ως εξής: στην περίπτωση της ισορροπίας, οι πιο αυστηρές συνθήκες υπάρχουν όταν πραγματοποιούνται μόνο σε ορισμένους δείκτες, δηλαδή μια αλλαγή σε οποιαδήποτε θερμοδυναμική παράμετρο θα οδηγήσει σε ανισορροπία. Αυτό σημαίνει ότι ο αριθμός των ελευθεριών l=0. Αντικαθιστώντας τις γνωστές τιμές των l και f, λαμβάνουμε k=1, δηλαδή ένα σύστημα στο οποίο τρεις φάσεις βρίσκονται σε ισορροπία μπορεί να αποτελείται από ένα συστατικό. Ένα χαρακτηριστικό παράδειγμα είναι το τριπλό σημείο του νερού, όπου ο πάγος, το υγρό νερό και ο ατμός βρίσκονται σε ισορροπία σε συγκεκριμένες θερμοκρασίες και πιέσεις.
Ταξινόμηση μετασχηματισμών φάσης
Αν αρχίσετε να αλλάζετε ορισμένες θερμοδυναμικές παραμέτρους σε ένα σύστημα σε ισορροπία, μπορείτε να παρατηρήσετε πώς μια φάση θα εξαφανιστεί και μια άλλη θα εμφανιστεί. Ένα απλό παράδειγμα αυτής της διαδικασίας είναι το λιώσιμο του πάγου όταν θερμαίνεται.
Δεδομένου ότι η εξίσωση Gibbs εξαρτάται μόνο από δύο μεταβλητές (πίεση και θερμοκρασία) και η μετάβαση φάσης περιλαμβάνει μια αλλαγή σε αυτές τις μεταβλητές, τότε μαθηματικά η μετάβαση μεταξύ των φάσεων μπορεί να περιγραφεί διαφοροποιώντας την ενέργεια Gibbs σε σχέση με την μεταβλητές. Ήταν αυτή η προσέγγιση που χρησιμοποιήθηκε από τον Αυστριακό φυσικό Paul Ehrenfest το 1933, όταν συνέταξε μια ταξινόμηση όλων των γνωστών θερμοδυναμικών διεργασιών που συμβαίνουν με μια αλλαγή στην ισορροπία φάσης.
Από τα βασικά της θερμοδυναμικής προκύπτει ότι η πρώτη παράγωγος της ενέργειας Gibbs σε σχέση με τη θερμοκρασία είναι ίση με τη μεταβολή της εντροπίας του συστήματος. Η παράγωγος της ενέργειας Gibbs ως προς την πίεση είναι ίση με τη μεταβολή του όγκου. Εάν, όταν αλλάζουν οι φάσεις στο σύστημα, η εντροπία ή ο όγκος υποστεί θραύση, δηλαδή αλλάζουν απότομα, τότε μιλούν για μετάβαση φάσης πρώτης τάξης.
Επιπλέον, οι δεύτερες παράγωγοι της ενέργειας Gibbs σε σχέση με τη θερμοκρασία και την πίεση είναι η θερμοχωρητικότητα και ο συντελεστής ογκομετρικής διαστολής, αντίστοιχα. Εάν ο μετασχηματισμός μεταξύ των φάσεων συνοδεύεται από ασυνέχεια στις τιμές των υποδεικνυόμενων φυσικών μεγεθών, τότε μιλάμε για μετάβαση φάσης δεύτερης τάξης.
Παραδείγματα μετασχηματισμών μεταξύ φάσεων

Υπάρχει ένας τεράστιος αριθμός διαφορετικών μεταβάσεων στη φύση. Στο πλαίσιο αυτής της ταξινόμησης, εντυπωσιακά παραδείγματα μεταπτώσεων του πρώτου είδους είναι οι διαδικασίες τήξης μετάλλων ή η συμπύκνωση υδρατμών από τον αέρα, όταν υπάρχει άλμα όγκου στο σύστημα.
Αν μιλάμε για μεταβάσεις δεύτερης τάξης, τότε εντυπωσιακά παραδείγματα είναι ο μετασχηματισμός του σιδήρου από μαγνητική σε παραμαγνητική κατάσταση σε θερμοκρασία768 ºC ή η μετατροπή ενός μεταλλικού αγωγού σε υπεραγώγιμη κατάσταση σε θερμοκρασίες κοντά στο απόλυτο μηδέν.
Εξισώσεις που περιγράφουν μεταβάσεις του πρώτου είδους
Στην πράξη, είναι συχνά απαραίτητο να γνωρίζουμε πώς η θερμοκρασία, η πίεση και η απορροφούμενη (απελευθερωμένη) ενέργεια αλλάζουν σε ένα σύστημα όταν συμβαίνουν μετασχηματισμοί φάσης σε αυτό. Για το σκοπό αυτό χρησιμοποιούνται δύο σημαντικές εξισώσεις. Λαμβάνονται με βάση τη γνώση των βασικών της θερμοδυναμικής:
- Ο τύπος του Clapeyron, ο οποίος καθιερώνει τη σχέση μεταξύ πίεσης και θερμοκρασίας κατά τη διάρκεια μετασχηματισμών μεταξύ διαφορετικών φάσεων.
- Φόρμουλα Clausius που συνδέει την απορροφούμενη (απελευθερωμένη) ενέργεια και τη θερμοκρασία του συστήματος κατά τη διάρκεια του μετασχηματισμού.
Η χρήση και των δύο εξισώσεων δεν αφορά μόνο τη λήψη ποσοτικών εξαρτήσεων φυσικών μεγεθών, αλλά και για τον προσδιορισμό του πρόσημου της κλίσης των καμπυλών ισορροπίας στα διαγράμματα φάσεων.
Εξίσωση για την περιγραφή μεταβάσεων δεύτερου είδους

Οι μεταβάσεις φάσεων του 1ου και του 2ου είδους περιγράφονται με διαφορετικές εξισώσεις, καθώς η εφαρμογή των εξισώσεων Clausius και Clausius για μεταβάσεις δεύτερης τάξης οδηγεί σε μαθηματική αβεβαιότητα.
Για να περιγραφεί το τελευταίο, χρησιμοποιούνται οι εξισώσεις Ehrenfest, οι οποίες καθορίζουν μια σχέση μεταξύ των μεταβολών της πίεσης και της θερμοκρασίας μέσω της γνώσης των αλλαγών στη θερμοχωρητικότητα και του συντελεστή ογκομετρικής διαστολής κατά τη διαδικασία μετασχηματισμού. Οι εξισώσεις Ehrenfest χρησιμοποιούνται για να περιγράψουν τις μεταβάσεις αγωγού-υπεραγωγού απουσία μαγνητικού πεδίου.
Σημασίαδιαγράμματα φάσεων
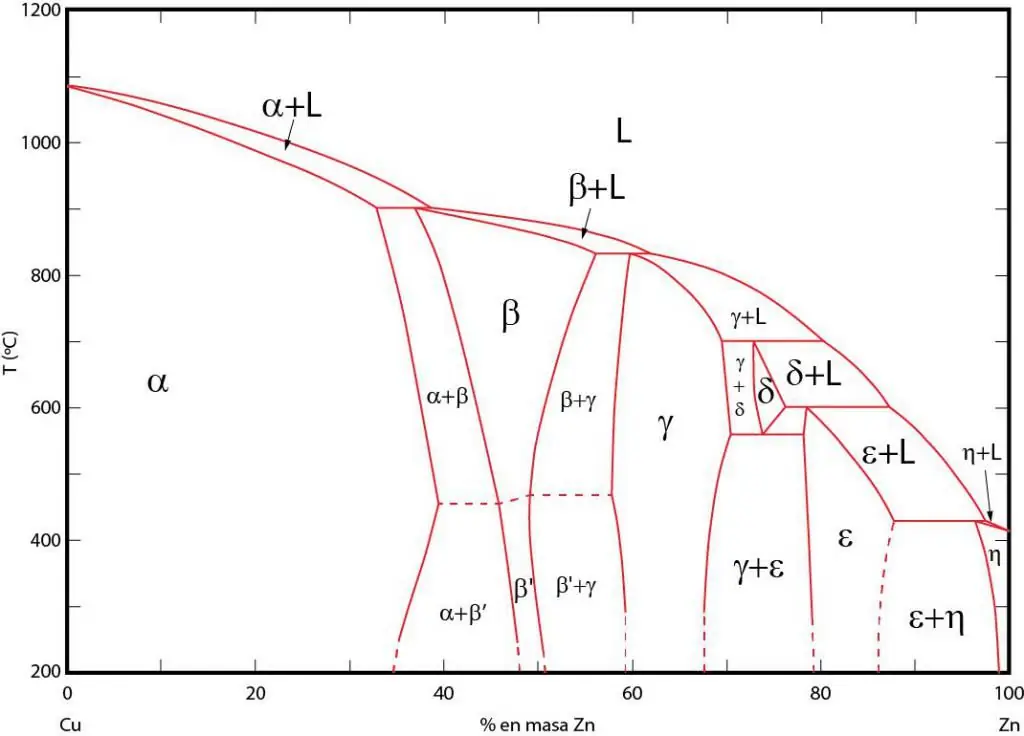
Τα διαγράμματα φάσεων είναι μια γραφική αναπαράσταση περιοχών στις οποίες οι αντίστοιχες φάσεις βρίσκονται σε ισορροπία. Αυτές οι περιοχές χωρίζονται με γραμμές ισορροπίας μεταξύ των φάσεων. Συχνά χρησιμοποιούνται διαγράμματα φάσης P-T (πίεση-θερμοκρασία), T-V (θερμοκρασία-όγκος) και P-V (πίεση-όγκος).
Η σημασία των διαγραμμάτων φάσης έγκειται στο γεγονός ότι σας επιτρέπουν να προβλέψετε σε ποια φάση θα βρίσκεται το σύστημα όταν αλλάξουν ανάλογα οι εξωτερικές συνθήκες. Αυτές οι πληροφορίες χρησιμοποιούνται στη θερμική επεξεργασία διαφόρων υλικών προκειμένου να ληφθεί μια δομή με επιθυμητές ιδιότητες.






