Μια γραμμική συνάρτηση είναι μια ευθεία γραμμή που χαράσσεται κατά μήκος μιας επιφάνειας. Μπορεί να χωριστεί σε διαφορετικούς τύπους και μοντέλα. Παρακάτω θα εξετάσουμε τους τύπους για την απόκτησή του, καθώς και την επίτευξη της τελειότητάς του στο επίπεδο. Στα σχέδια, μπορείτε να το επαληθεύσετε πλήρως και να καταλάβετε πώς πρέπει να φαίνεται.
Γραμμική συνάρτηση y=kx + b
Αυτή η τιμή είναι ένα ακριβές μέτρο μιας μεταβλητής σε μία προβολή. Η αύξηση αναφέρεται στη βασική ιδιότητα μιας γραμμικής συνάρτησης, γίνεται ανάλογη με το αυξημένο όρισμα. Με άλλα λόγια, η συνάρτηση αντιπροσωπεύει μια γενίκευση της ευθείας αναλογικότητας. Μια ευθεία γραμμή είναι ένα γράφημα μιας γραμμικής συνάρτησης. Από εδώ προέρχεται το όνομά του. Μια πραγματική μεταβλητή αγγίζει μια άλλη πραγματική συνάρτηση.
Ιδιότητες
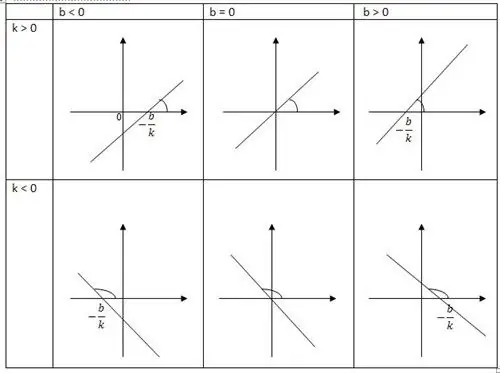
Γραμμική συνάρτηση είναι μια γεννήτρια μιας ευθείας γραμμής, η οποία έχει θετική κατεύθυνση του άξονα x. Ένας από τους καθοριστικούς παράγοντες κλίσης του είναι ο k, καθορίζει την εφαπτομένη της γωνίας α. Η ευθεία που σχηματίζεται στη θετική κατεύθυνση του άξονα x είναι k. Η άλλη συντεταγμένη b δείχνεισυντεταγμένες σημείου, καθώς και η τομή της ευθείας με τον άξονα.
Τι είναι οι μη γραμμικές συναρτήσεις;
Οι συναρτήσεις που δεν είναι γραμμικές ονομάζονται μη γραμμικές. Αυτή είναι μια μαθηματική σχέση μεταξύ μεταβλητών. Οι μη γραμμικές δεν μπορούν να εκφραστούν ως y=ax + b. Αυτός ο όρος χρησιμοποιείται σε εκείνες τις στιγμές που είναι απαραίτητο να μελετηθεί η γενική περίπτωση. Αυτή η διαδικασία ξεκινά με τους χαμηλότερους βαθμούς. Στην περίπτωση αυτή, λαμβάνονται υπόψη οι δευτεροβάθμιες διορθώσεις. Μια τέτοια συνάρτηση έχει συνεχή καμπυλότητα.
Η θεωρούμενη μη γραμμική εξίσωση είναι αυθαίρετη. Ένα παράδειγμα μη γραμμικής συνάρτησης είναι το y=x2. Συχνά χρησιμοποιούνται οι όροι «γραμμική συνάρτηση», με μια τελειοποίηση και την προσθήκη του «ομογενούς». Μπορεί να εφαρμοστεί σε μια ακριβή γραμμική αντιστοίχιση του Χ, που είναι ένας διανυσματικός χώρος. Μια γραμμική συνάρτηση είναι ολόκληρο το σύστημα όπως αυτή.






