Η θερμοδυναμική της κατάστασης των αέριων συσσωματωμάτων της ύλης είναι ένας σημαντικός κλάδος της φυσικής που μελετά τη θερμοδυναμική ισορροπία και τις οιονεί στατικές μεταπτώσεις στα συστήματα. Το κύριο μοντέλο στο οποίο βασίζονται οι προβλέψεις της συμπεριφοράς των συστημάτων είναι το μοντέλο ιδανικού αερίου. Με τη χρήση του προέκυψε η εξίσωση Mendeleev-Clapeyron. Σκεφτείτε το στο άρθρο.
Ιδανικό αέριο
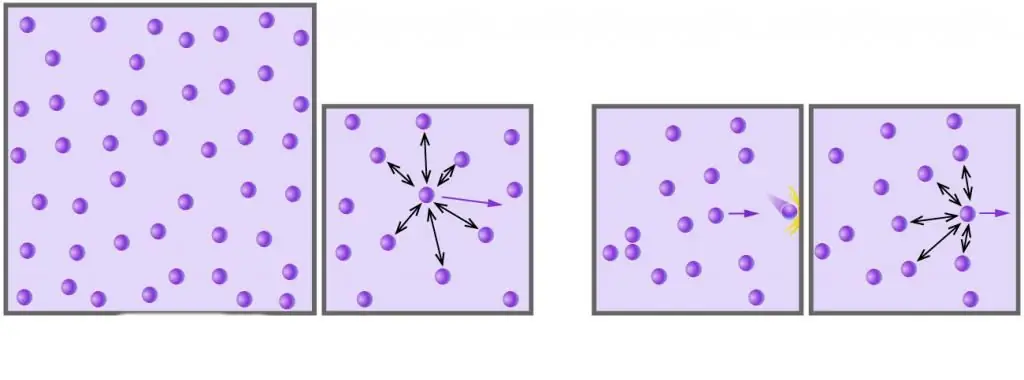
Όπως γνωρίζετε, όλα τα πραγματικά αέρια αποτελούνται από μόρια ή άτομα, οι αποστάσεις μεταξύ των οποίων είναι πολύ μεγάλες σε σύγκριση με το μέγεθός τους σε χαμηλές πιέσεις. Επιπλέον, σε υψηλές θερμοκρασίες, σε απόλυτη κλίμακα, η κινητική ενέργεια των μορίων υπερβαίνει τη δυναμική τους ενέργεια που σχετίζεται με ασθενείς αλληλεπιδράσεις διπόλου-διπόλου (εάν, εκτός από αυτές τις αλληλεπιδράσεις, υπάρχουν και άλλοι τύποι χημικών δεσμών, για παράδειγμα, ιονικοί ή υδρογόνο, τότε συμβάλλουν σημαντικά στη δυνητική συνιστώσα της ενέργειας του εσωτερικού συστήματος).
ΛόγωΓια πολλά πραγματικά αέρια υπό συνθήκες κοντά στο κανονικό, μπορεί κανείς να παραμελήσει τις εσωτερικές τους αλληλεπιδράσεις και το μέγεθος των σωματιδίων. Αυτές οι δύο κύριες προσεγγίσεις αποτελούν το ιδανικό μοντέλο αερίου.
Η εξίσωση του Μεντελέεφ στη φυσική

Είναι πιο σωστό και δίκαιο να ονομάσουμε αυτή την εξίσωση νόμο Clapeyron-Mendeleev. Γεγονός είναι ότι ηχογραφήθηκε για πρώτη φορά από τον Γάλλο μηχανικό Emile Clapeyron το 1834. Αυτό το έκανε αναλύοντας τους νόμους των αερίων των Boyle-Mariotte, Gay-Lussac και Charles που ανακαλύφθηκαν στις αρχές του 19ου αιώνα.
Η αξία του Ρώσου χημικού Dmitry Mendeleev έγκειται στο γεγονός ότι έδωσε στην εξίσωση μια σύγχρονη και εύχρηστη μαθηματική μορφή. Συγκεκριμένα, ο Mendeleev εισήγαγε στην εξίσωση μια σταθερά για όλα τα αέρια R=8, 314 J/(molK). Ο ίδιος ο Clapeyron χρησιμοποίησε μια σειρά από εμπειρικές σταθερές που δυσκολεύουν την υπολογιστική διαδικασία.
Η εξίσωση Mendeleev-Clapeyron γράφεται ως εξής:
PV=nRT.
Αυτή η ισότητα σημαίνει ότι το γινόμενο της πίεσης P και του όγκου V στην αριστερή πλευρά της παράστασης είναι πάντα ανάλογο με το γινόμενο της απόλυτης θερμοκρασίας T και την ποσότητα της ουσίας n στην αριστερή πλευρά.
Η έκφραση υπό μελέτη σάς επιτρέπει να λάβετε οποιονδήποτε νόμο περί αερίων εάν διορθώσετε δύο από τις τέσσερις παραμέτρους του. Στην περίπτωση των ισοδιεργασιών μελετώνται κλειστά συστήματα στα οποία δεν υπάρχει ανταλλαγή ύλης με το περιβάλλον (n=const). Αυτές οι διεργασίες χαρακτηρίζονται από μία μόνο σταθερή θερμοδυναμική παράμετρο (T, P ή V).

Παράδειγμα προβλήματος
Τώρα ας λύσουμε το πρόβλημα στην εξίσωση Mendeleev-Clapeyron. Είναι γνωστό ότι το οξυγόνο βάρους 500 γραμμαρίων βρίσκεται σε κύλινδρο όγκου 100 λίτρων σε πίεση 2 ατμοσφαιρών. Ποια είναι η θερμοκρασία στο μπαλόνι, δεδομένου ότι το σύστημα βρίσκεται σε θερμοδυναμική ισορροπία.
Υπενθυμίζουμε ότι, σύμφωνα με τον ορισμό, η ποσότητα μιας ουσίας υπολογίζεται με τον τύπο:
n=m/M.
Όπου m είναι η μάζα όλων των σωματιδίων του συστήματος, M είναι η μέση μοριακή τους μάζα. Αυτή η ισότητα μας επιτρέπει να ξαναγράψουμε την εξίσωση Mendeleev με την ακόλουθη μορφή:
PV=mRT/M.
Πού βρίσκουμε τον τύπο εργασίας για αυτήν την εργασία:
T=PVM/(mR).
Απομένει να μετατρέψουμε όλες τις ποσότητες σε μονάδες SI και να τις αντικαταστήσουμε σε αυτήν την έκφραση:
T=21013250, 10, 032/(0, 58, 314)=156 K.
Η υπολογισμένη θερμοκρασία είναι -117 oC. Αν και το οξυγόνο σε αυτή τη θερμοκρασία είναι ακόμα αέριο (συμπυκνώνεται στους -182,96 oC), υπό τέτοιες συνθήκες το μοντέλο ιδανικού αερίου μπορεί να χρησιμοποιηθεί μόνο για να ληφθεί μια ποιοτική εκτίμηση της υπολογιζόμενης τιμής.






